Question

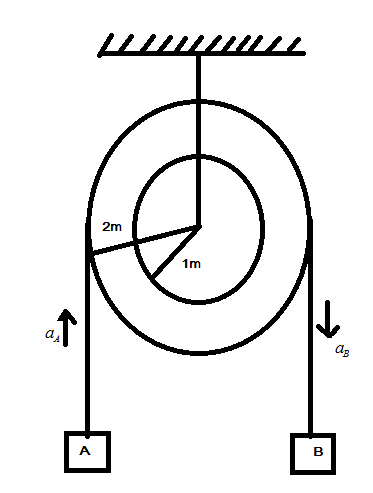
In the pulley system shown, if radii of the double pulley system are $ 2m $ and $ 1m $ respectively are as shown. The system is in equilibrium. The mass of two blocks A and B is :
(A) $ 1:5 $
(B) $ 1:3 $
(C) $ 1:4 $
(D) $ 1:2 $

Answer 1

Hint :Here, we have been given the diagram as shown in the figure and in here we have to assume that the acceleration of the block A is $ {a_A} $ and for block B is $ {a_B} $ . The given system is in equilibrium so masses are equal.

Complete Step By Step Answer:
Let us assume that the system is moving and the acceleration for block A be $ {a_A} $ and that of block B be $ {a_B} $ . According to the radii of the pulleys we have:
Acceleration of block B is $ {a_B} = \dfrac{{{a_A}}}{2} $ .
Now, the system being in equilibrium we have forces acting on them as equal.
 $ {F_A} = {F_B} $
 $ \Rightarrow {m_A}{a_A} = {m_B}{a_B} $
 $ \Rightarrow {m_A}{a_A} = {m_B}\dfrac{{{a_A}}}{2} $ …(since, $ {a_B} = \dfrac{{{a_A}}}{2} $ )
 $ \Rightarrow \dfrac{{{m_A}}}{{{m_B}}} = \dfrac{1}{2} $
Thus the two masses are in the ratio of $ 1:2 $ .
The correct answer is option D.

Note :
Here, we have given the blocks are in equilibrium and we have to assume that the acceleration of both the blocks are also in the ratio of $ 1:2 $ since the radii of the pulleys are $ 2m $ and $ 1m $ . According to this information we have determined the acceleration, in this way we have calculated the acceleration as well as the ratio of masses. Equilibrium system possesses equal forces. We have calculated mass ratio with help of equating forces.