Question

In the right-angle triangle, the side opposite to the angle having measure 30 degrees is …………………….to the hypotenuse
A). Three times
B). Half
C). Double
D). Fourth part

Answer 1

Hint: In this question assume equilateral triangle ABC and draw an altitude from point A on BC such that it bisects BC at D and also $\angle A$, using this information to approach the solution of the question.

Complete step-by-step solution:

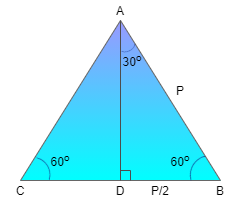
Let’s take an equilateral triangle ABC as shown in the figure above
So, for an equilateral triangle all sides are equal hence AB = BC = CA = p meters and since it is an equilateral triangle hence $\angle A = \angle B = \angle C = {60^\circ }$
Now let’s draw an altitude from point A on BC such that it bisects BC at D and also bisects angle A.
Now we get two right angles $\Delta $ that is $\Delta ACD$ and $\Delta ADB$such that $\angle CAD = \angle DAB = {30^\circ }$.
Clearly, $DB = \dfrac{p}{2}$ as the altitude from point A to BC bisects it in two equal halves.
Now as Ab is the hypotenuse and it is p meters and DB is $\dfrac{p}{2}$ meters
So, we can say that $DB = \dfrac{1}{2}AB$
Hence the side opposite to the angles having measure 30 degree is half the length of hypotenuse.

Note: Whenever we come across such problem statements we simply need to think of equilateral triangles as they have the property that the measure of the angle in them is 60 degrees. Moreover, stretching a basic altitude which bisects the side on which it is drawn always helps in simplification.