Question

In triangle ABC, right angled at B, $15\sin A=12$. Find the other five trigonometric ratios of the angle A. also find the six ratios of the angle C.

Answer 1

Hint:Divide both sides of the given equation by 15. Assume that in the obtained function: $\sin A=\dfrac{12}{15}$. 12 is the length of perpendicular and 15 is the length of hypotenuse of the right angle triangle. Use Pythagoras theorem given by: $\text{hypotenus}{{\text{e}}^{\text{2}}}=\text{bas}{{\text{e}}^{\text{2}}}+\text{perpendicula}{{\text{r}}^{\text{2}}}$, to determine the length of the base of the right angle triangle. Now, find $\cos A$ by taking the ratio of base and hypotenuse. To find $\tan A$ take the ratio of $\sin A$ and $\cos A$. Take the reciprocal of $\cos A$, $\sin A$ and $\tan A$ to find the value of $\sec A$, $\cos ecA$ and $\cot A$ respectively. Use the complementary angle formula: $\sin \left( {{90}^{\circ }}-A \right)=\cos C$, because $A+C={{90}^{\circ }}$. Similarly apply it for cosine and tangent of angle A to determine the ratios for C.

Complete step-by-step answer:
We have been provided with the trigonometric ratio relation: $15\sin A=12$. Dividing both sides by 15, we get, $\sin A=\dfrac{12}{15}$.
We know that, $\sin \theta =\dfrac{\text{Perpendicular}}{\text{Hypotenuse}}$. Therefore, on comparing it with the above provided ratio, we have, 12 as the length of perpendicular and 15 as the length of hypotenuse of a right angle triangle.

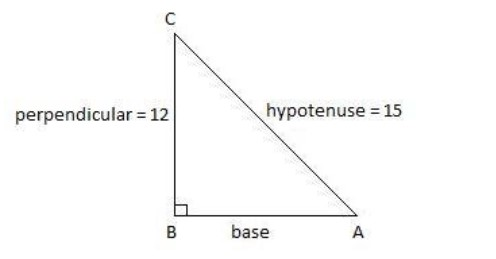
Now, using Pythagoras theorem: $\text{hypotenus}{{\text{e}}^{\text{2}}}=\text{bas}{{\text{e}}^{\text{2}}}+\text{perpendicula}{{\text{r}}^{\text{2}}}$, we get,
\[\begin{align}
  & \text{bas}{{\text{e}}^{\text{2}}}=\text{hypotenus}{{\text{e}}^{\text{2}}}-\text{perpendicula}{{\text{r}}^{\text{2}}} \\
 & \Rightarrow \text{base}=\sqrt{\text{hypotenus}{{\text{e}}^{\text{2}}}-\text{perpendicula}{{\text{r}}^{\text{2}}}} \\
 & \Rightarrow \text{base}=\sqrt{{{15}^{\text{2}}}-{{12}^{\text{2}}}} \\
 & \Rightarrow \text{base}=\sqrt{225-144} \\
 & \Rightarrow \text{base}=\sqrt{169} \\
 & \Rightarrow \text{base}=13 \\
\end{align}\]
We know that, $\cos A=\dfrac{\text{Base}}{\text{Hypotenuse}}$
\[\Rightarrow \cos A=\dfrac{13}{15}\]
Also, $\tan A=\dfrac{\text{Perpendicular}}{\text{Base}}$
$\Rightarrow \tan A=\dfrac{8}{15}$
Now, take the reciprocal of $\cos A$, $\sin A$ and $\tan A$ to find the value of $\sec A$, $\cos ecA$ and $\cot A$ respectively.
$\begin{align}
  & \sec A=\dfrac{1}{\cos A} \\
 & \Rightarrow \sec A=\dfrac{15}{13} \\
\end{align}$
$\begin{align}
  & \cos ecA=\dfrac{1}{\sin A} \\
 & \Rightarrow \cos ecA=\dfrac{15}{12} \\
\end{align}$
$\begin{align}
  & \cot A=\dfrac{1}{\tan A} \\
 & \Rightarrow \cot A=\dfrac{15}{8} \\
\end{align}$
Now, we have been given that angle B is 90 degrees. Therefore, the sum of angle A and angle C must be 90 degrees. Hence, angle A and angle C are complementary angles. So,
$\begin{align}
  & A+C={{90}^{\circ }} \\
 & \Rightarrow C={{90}^{\circ }}-A \\
\end{align}$
Taking sine function both sides, we get,
$\sin C=\sin \left( {{90}^{\circ }}-A \right)$
Using the identity: $\sin \left( {{90}^{\circ }}-\theta \right)=\cos \theta $, we get,
$\begin{align}
  & \sin C=\cos A \\
 & \Rightarrow \sin C=\dfrac{13}{15} \\
\end{align}$
Similarly,
$\begin{align}
  & \cos C=\cos \left( {{90}^{\circ }}-A \right) \\
 & \Rightarrow \cos C=\sin A \\
 & \Rightarrow \cos C=\dfrac{12}{15} \\
\end{align}$
$\begin{align}
  & \tan C=\dfrac{\sin C}{\cos C} \\
 & \Rightarrow \tan C=\dfrac{\dfrac{13}{15}}{\dfrac{12}{15}} \\
 & \Rightarrow \tan C=\dfrac{13}{12} \\
\end{align}$
Now, take the reciprocal of $\cos C$, $\sin C$ and $\tan C$ to find the value of $\sec C$,\[\] $\cos ecC$ and $\cot C$ respectively.
$\begin{align}
  & \sec C=\dfrac{1}{\cos C} \\
 & \Rightarrow \sec C=\dfrac{15}{12} \\
\end{align}$
$\begin{align}
  & \cos ecC=\dfrac{1}{\sin C} \\
 & \Rightarrow \cos ecC=\dfrac{15}{13} \\
\end{align}$
$\begin{align}
  & \cot C=\dfrac{1}{\tan C} \\
 & \Rightarrow \cot A=\dfrac{12}{13} \\
\end{align}$

Note: Here, we have used Pythagoras theorem to determine the base of the triangle to find other trigonometric ratios. One may note that, $\sec A$ is the ratio of length of hypotenuse and base, $\cos ecA$ is the ratio of length of perpendicular and base, and $\cot A$ is the ratio of length of base and hypotenuse. So, these ratios can also be found without taking the reciprocals.