Question

In which polyhedron has $6$ faces, $8$ vertices and $12$ edges?
A) Cube
B) Sphere
C) Triangular Prism
D) Cone

Answer 1

Hint: We have to find which polyhedron has $6$ faces, $8$ vertices and $12$ edges. Polyhedron can be defined as a three- dimensional structure which is made up of a finite number of polygonal faces. Generally, polyhedrons are named according to the number of faces.

Complete step by step answer:
In Euclidean geometry a polyhedron can be defined as a three- dimensional structure which is made up of a finite number of polygonal faces and they are named according to the number of faces. The boundary which is in between the interior and the exterior of a solid is a polyhedron.
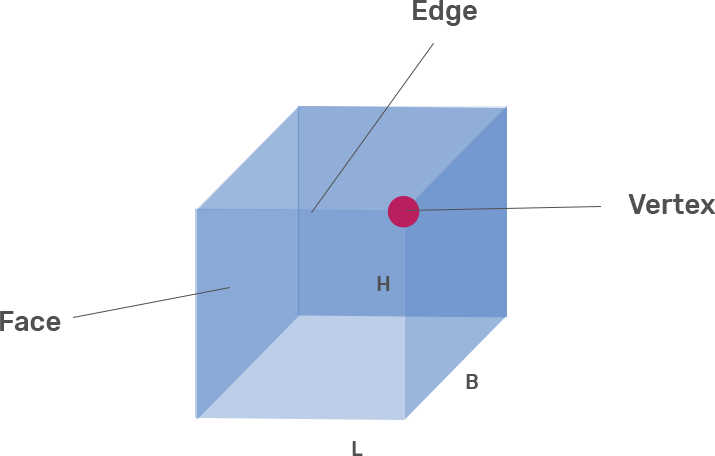
The polyhedron is made up of three parts namely Face, Vertex and Edge.
A face is a flat surface that makes up a polyhedron which is a regular polygon.
An edge is the region where the two flat surfaces meet to form a line segment.
A vertex which is also known as a corner is a point of intersection of the edges of the polyhedron.
Here, we have to find which polyhedron has $6$ faces, $8$ vertices and $12$ edges.
A cube is a polyhedron which has $6$ faces, $8$ vertices and $12$ edges and it has three squares that meet at each vertex.

Hence, Option (A) is correct.

Note:
A sphere has $1$ face, $0$ edge and $0$ vertex.
A triangular prism has $5$ faces, $6$ vertices and $9$ edges.
A cone has $2$ faces, $1$edge and $1$ vertex.
In Euclidean geometry there is a theorem known as Euler theorem named after Leonhard Euler which gives us a relation between the number of faces, vertices and edges of any polyhedron. The formula is given by $F+V=E+2$ where $F$ denotes the number of faces, $V$ denotes the number of vertices and $E$ denotes the number of edges of polyhedrons.