
In Young's experiment the monochromatic light is used to illuminate two slits A and B as shown in figure. Interference fringes are observed on a screen placed in front of the slits. Now a thin glass plate is placed normally in the path of the beam coming from the slit A, then.
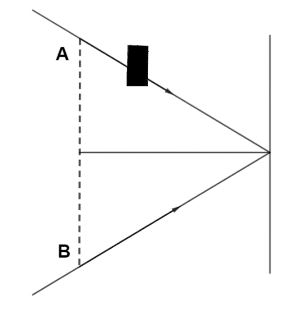
A. there will be no change in fringe width.
B. fringe width will decrease
C. fringe width will increase
D. fringes will disappear

Answer
404.7k+ views
1 likes
Hint: In order to solve this question, we will first draw the diagram by tracing the path of two light waves interfering due to slits at A and B at some point on screen and then calculate the total path difference of these two light rays and using general condition for bright fringe we will calculate fringe width.
Formula used:
If
Fringe width is calculated by using
where
Fringe width for Young’s double slit experiment is,
Complete step by step answer:
Let us first draw the diagram where slits are represented by
So, if there were no glass plate then from young’s double slit experiment we know that the path difference is written as
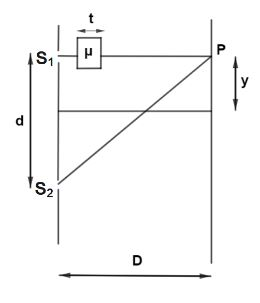
Now, when thing glass plate is placed then there will be extra path difference due to this glass plate along the path
Now, for
Now, let us find the value of y for
For fringe width we have,
On putting the values we get,
on solving we get,
Hence, the correct option is A.
Note: It should be remembered that, when a glass plate is placed on the path of wave the fringe width remain same but the position of bright fringes gets shifted in the direction where glass plate was placed and the amount to which position of fringes gets shifted is
Formula used:
If
Fringe width is calculated by using
where
Fringe width for Young’s double slit experiment is,
Complete step by step answer:
Let us first draw the diagram where slits are represented by
So, if there were no glass plate then from young’s double slit experiment we know that the path difference is written as

Now, when thing glass plate is placed then there will be extra path difference due to this glass plate along the path
Now, for
Now, let us find the value of y for
For fringe width we have,
On putting the values we get,
on solving we get,
Hence, the correct option is A.
Note: It should be remembered that, when a glass plate is placed on the path of wave the fringe width remain same but the position of bright fringes gets shifted in the direction where glass plate was placed and the amount to which position of fringes gets shifted is
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Which one of the following is a true fish A Jellyfish class 12 biology CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write the difference between solid liquid and gas class 12 chemistry CBSE




