Question

What do you infer from the experiment which you did with concave mirrors and measured the distance of the object and distance of the image?

Answer 1

Hint: Experiment we perform with a concave mirror is that we will keep the object at principal focus, at the centre of curvature etc to examine the formation of the image at different places with different size and erection or inversion. In this problem we will keep the object beyond $C$.
Distance of the object from the principal pole of the mirror is taken as ‘$u$’.
Distance of the image from the principal pole of the mirror is taken as ‘$v$’.

Complete step by step answer:
We will keep objects at different places to examine the image formation.

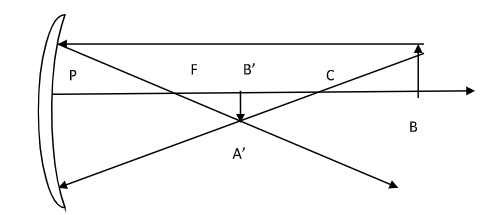
In the above figure we have kept the object beyond $C$.
Let’s get familiar with the terms related to mirror first.
Principal focus: the point at which a narrow beam of light incident on the mirror parallel to its principal axis, after reflection from the mirror, meets or appears to come from is called the principal focus. It is denoted by $F$.
Centre of curvature: The centre of the sphere of which the mirror forms a part is called the centre of curvature of the mirror. It is denoted by $C$.
Principal axis: the line joining the pole and the centre of curvature of the mirror is called the principal axis of the mirror.
Pole: the centre of the spherical mirror is called its pole.
In the above figure our object is placed beyond $C$ and all the distances are taken in the direction of the incident ray (which are positive and distances which are taken opposite to the direction of incident ray are taken as negative).
Image is formed between the principal focus and centre of curvature which is inverted and highly diminished.
Similarly, if we keep the object between principal focus and centre of curvature, the image will be formed beyond $C$ and will be large and erect.
Mirror formula is given as:
$\dfrac{1}{f} = \dfrac{1}{u} + \dfrac{1}{v}$ ($f$ is the focal length, $u$ is the distance of object and $v$ is the distance of image all are measured in the direction of incident ray and are taken as positive).

Note:
Concave mirrors are used as reflectors in cinema projectors, used to construct reflecting type astronomical telescopes, as parabolic mirrors in search lights. Concave mirrors are called converging mirrors because they converge the incident light falls on it.