Question

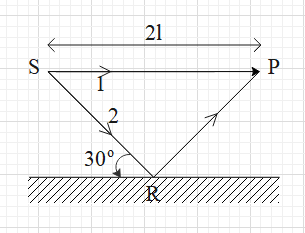
Interference pattern is observed at P due to superposition of two waves coming out from a source ‘S’ as shown in the figure. The value of ‘l’ for which maxima is obtained at ‘P’ is (R is perfect reflecting surface)

$\text{A}\text{. }l=\dfrac{2n\lambda }{\sqrt{3}-1}$
$\text{B}\text{. }l=\dfrac{(2n-1)\lambda }{2\left( \sqrt{3}-1 \right)}$
$\text{C}\text{. }l=\dfrac{(2n-1)\lambda \sqrt{3}}{4\left( 2-\sqrt{3} \right)}$
$\text{D}\text{. }l=\dfrac{(2n-1)\lambda }{\sqrt{3}-1}$

Answer 1

Hint: When two waves from the same source superimpose at a point, maxima is obtained at the point if the path difference between the two waves is an integer multiple of the wavelength of the wave. Find the path of both waves. Find the difference in both and find the value of l.

Formula used:’
$\Delta x=n\lambda $

Complete step-by-step answer:
When two waves from the same source superimpose at a point, maxima is obtained at the point if the path difference between the two waves is an integer multiple of the wavelength of the wave.
i.e. $\Delta x=n\lambda $, $\Delta x$ is the path difference between the waves, n is an integer and $\lambda $ is the wavelength of the waves.
The wave 1 is directly reaching the point P. Therefore, the path covered by it is equal to ${{x}_{1}}=2l$.
Let us measure the path covered by wave 2. We can see that this wave reflects at surface R and then reaches point P.
From the figure the incident angle (i) at the surface R is ${{60}^{\circ }}$. From the laws of reflection, we know that the reflection angle and the incident angle are equal. Therefore, $r={{60}^{\circ }}$.

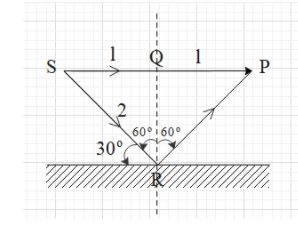
Now, consider $\Delta SQR$.
In this triangle, $\dfrac{SQ}{SR}=\sin i$
$\Rightarrow \dfrac{l}{SR}=\sin {{60}^{\circ }}=\dfrac{\sqrt{3}}{2}$
$\Rightarrow SR=\dfrac{2l}{\sqrt{3}}$.
The $\Delta SPR$ is an isosceles triangle. Therefore, SR = PR.
The path covered by the wave 2 is $SR+PR=\dfrac{2l}{\sqrt{3}}+\dfrac{2l}{\sqrt{3}}=\dfrac{4l}{\sqrt{3}}$.
However, the wave 2 is reflecting at surface R, and will change its phase by $\pi $. An addition of a phase by $\pi $ is equivalent to an addition of a path by $\dfrac{\lambda }{2}$.
Therefore, the total path of wave 2 is ${{x}_{2}}=\dfrac{4l}{\sqrt{3}}+\dfrac{\lambda }{2}$.
The path difference will be $\Delta x={{x}_{2}}-{{x}_{1}}=\dfrac{4l}{\sqrt{3}}+\dfrac{\lambda }{2}-2l$
And $\Delta x=n\lambda $.
$\Rightarrow n\lambda =\dfrac{4l}{\sqrt{3}}+\dfrac{\lambda }{2}-2l$
$\Rightarrow \dfrac{4l}{\sqrt{3}}-2l=n\lambda -\dfrac{\lambda }{2}$
$\Rightarrow \left( \dfrac{4}{\sqrt{3}}-2 \right)l=\left( n-\dfrac{1}{2} \right)\lambda $
$\Rightarrow \left( \dfrac{4-2\sqrt{3}}{\sqrt{3}} \right)l=\left( \dfrac{2n-1}{2} \right)\lambda $
$\Rightarrow l=\left( \dfrac{\sqrt{3}}{4-2\sqrt{3}} \right)\left( \dfrac{2n-1}{2} \right)\lambda $
$\Rightarrow l=\dfrac{(2n-1)\lambda \sqrt{3}}{4\left( 2-\sqrt{3} \right)}$

So, the correct answer is “Option C”.

Note: If we do not know that a change in phase by $\pi $ is equivalent to a change in path by $\dfrac{\lambda }{2}$, then we can use the relation between change in phase and the change in path. Phase is denoted by $\phi $. And the relation is given as $\dfrac{\Delta \phi }{2\pi }=\dfrac{\Delta x}{\lambda }$.