Question

Internal energy of an ideal gas depends upon:
A. Pressure
B. Temperature
C. Volume
D. None of these

Answer 1

Hint: An ideal gas is the gas which has perfectly elastic collisions between its particles and the intermolecular forces of attraction are absent in it. The ideal gas is a hypothetical concept as there is no such gas which doesn't have intermolecular forces of attraction at all. Also, the particles in an ideal gas do not occupy any volume.

Complete step by step solution:
The internal energy of a gas refers to the energy due to the random and disordered motion of the gas molecules or particles. The internal energy for any system is denoted by U and expressed in joules (J).

The internal energy of a system is the sum of both kinetic and potential energy of that system. For an ideal gas, the potential energy is zero as there is no particle-particle interaction. Therefore, the internal energy of an ideal gas equals to that of only kinetic energy of an ideal gas.

The kinetic energy of an ideal gas is the sum of kinetic energies of the particles in that gas. The kinetic energy of a gas is because of the motion of its particle such as translation, rotational and vibrational. This also means that the change in kinetic energies of the particles in an ideal gas will lead to the changes in its internal energy.

According to kinetic molecular theory assumes that the temperature of a gas is directly proportional to the average kinetic energy of its particles. For a monatomic gas, the internal energy is the translational kinetic energy of the gas.
According to the kinetic theory of gases, the internal energy for an ideal gas is,
$U = \dfrac{3}{2}nRT$…………….(1)
The value of n is 1 here, so the formula (1) can be written as:
$U = \dfrac{3}{2}RT$

In an ideal gas the inter-molecular collisions are assumed to be absent and the collisions are perfectly elastic. Thus, the gas possesses only translational kinetic energy and hence the internal energy of the ideal gas depends only on temperature. Hence, the internal energy of an ideal gas is therefore directly proportional to the temperature of the gas.
Hence, internal energy of an ideal gas depends on only temperature.

Therefore, the correct option is option (B).

Note: The scientist Gay-Lussac performed a simple experiment to shown that an internal energy of an ideal gas is depends only on its temperature.
During the experiment, two containers were connected by a pipe and valve. The containers were named as 1 and 2.
Container 1 was filled with an ideal gas and container 2 was kept completely empty. The scientists ensured that the system is perfectly insulated from its surroundings.

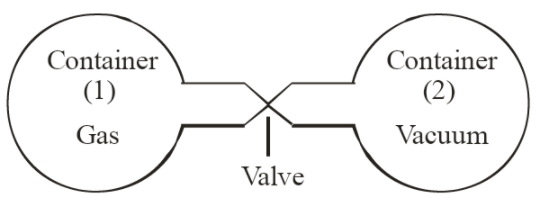
When the valve is opened, the gas in container 1 expands into vacuum 2. During this, the pressure and volume of the gas changes but temperature remain constant. As there was no exchange of work or heat with surrounding, the internal energy remained the same during this process. Thus, the internal energy of an ideal gas is only a function of its temperature.