Question

K, L, M, N are points on sides AB, BC, CD, DA respectively of square ABCD such that AK=BL=CM=DN. Prove that KLMN is a square.

Answer 1

Hint: To prove that KLMN is a square we have to prove that the sides are the same and all angles are of\[{90^ \circ }\].
Need to prove both because a rhombus is also having all sides the same.

Complete step-by-step answer:
Let’s draw the diagram first.

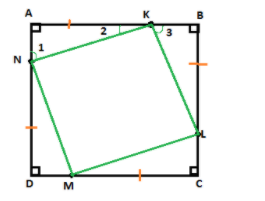
Here it is given that ABCD is a square.
So AB=BC=CD=DA ……(1)
Also, AK=BL=CM=DN ……..(2)
Now subtract equation 2 from 1.
AB-AK=BC-BL=CD-CM=DA-DN
Observing figure above,
AB-AK=BK
BC-BL=CL
CD-CM=DM
DA-DN=NA
Thus, BK=CL=DM=NA
And BL=CM=DN=AK
Squaring and adding,
\[B{K^2} + B{L^2} = C{L^2} + C{M^2} = D{M^2} + D{N^2} = A{N^2} + A{K^2}\]
Since all four angles of ABCD square are\[{90^ \circ }\].
So applying Pythagoras theorem above equation will become,
\[
  B{K^2} + B{L^2} = K{L^2} \\
  C{L^2} + C{M^2} = L{M^2} \\
  D{M^2} + D{N^2} = M{N^2} \\
  A{N^2} + A{K^2} = N{K^2} \\
\]
Thus,
\[K{L^2} = L{M^2} = M{N^2} = N{K^2}\]
Taking square root on above equation,
\[KL = LM = MN = NK\]
This proves all four sides are the same. But a rhombus is also having all four sides the same. So need to prove that all four angles are\[{90^ \circ }\].
In \[\vartriangle ANK\] and \[\vartriangle BKL\]
\[
  AK \cong BL \\
  AN \cong BK \\
  \angle A \cong \angle B \\
  \vartriangle ANK \cong \vartriangle BKL \\
  \angle ANK = \angle BKL \\
\]
But \[\angle 1 + \angle 2 = {90^ \circ }\]
From figure
\[
  \angle 1 = \angle 3 \\
  \angle 3 + \angle 2 = {90^ \circ } \\
\]
Thus the remaining angle is of \[{90^ \circ }\].
That is \[\angle NKL = {90^ \circ }\].
Similarly, all other angles are of \[{90^ \circ }\].
Thus KLMN is a square.

Note: In this geometrical problem we need to prove that all four sides are same along with all four angles are of \[{90^ \circ }\]. The equation we form is the key to prove the statement.