Question

How do we know we have to shade the above line or below the line?

Answer 1

Hint: In order to know the answer to the given question that How do we know we have to shade the above line or below the line is, the sign of the inequality will let you know which half-plane to shade or which is the appropriate region to be shade.

Complete step by step solution:
According to the question, we have to find out when to shade the above line or below the line,
This question arises when we have a problem of One linear inequality in two variables. This problem basically divides the plane into two half-planes. To graph the inequality, graph the equation of the boundary.  Use a solid line if the symbol \[\leq \] or \[\geq\] is used because the boundary is included in the solution.  Use a dashed line if < or   >   is used to indicate that the boundary is not part of the solution. Shade the appropriate region. Unless you are graphing a vertical line the sign of the inequality will let you know which half-plane to shade.  If the symbol \[\geq \] or > is used, shade above the line.  If the symbol \[\leq \] or < is used shade below the line.

For better understanding consider following to examples:
Example 1: \[y\geq 4x+3\]
You would draw the line \[y=4x+3\] and shade above the line, since \[y\]is also greater than \[4x+3\]. As shown in the graph below:

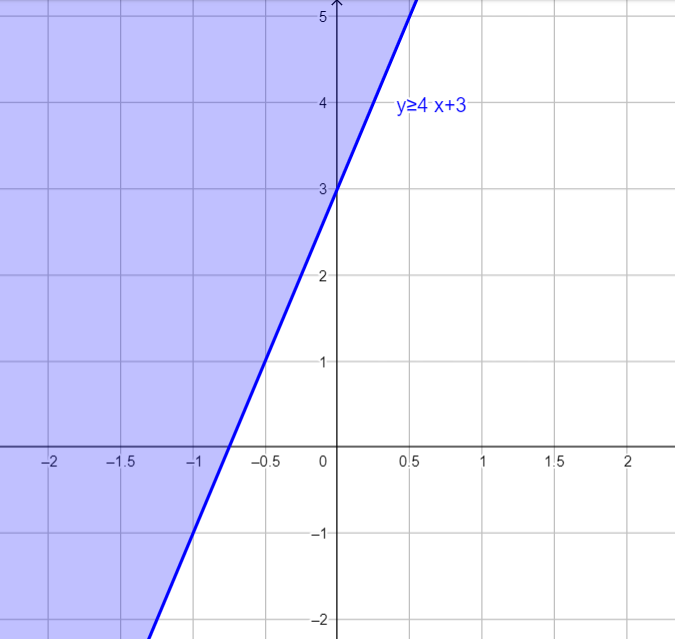
Example 2: \[yYou would draw the line \[y=x-2\] as a dashed line, then shade below the line since \[y\] is less than \[x-2\]. As shown in the graph below:

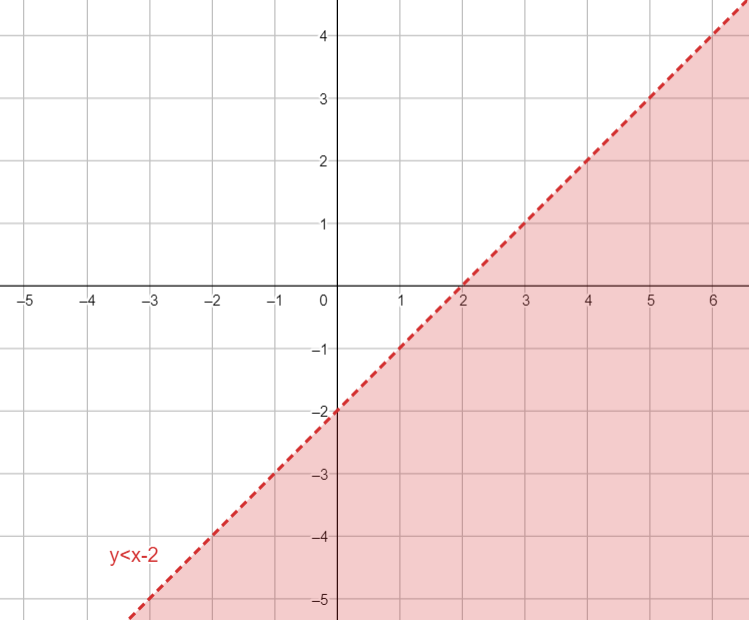
Therefore, the symbol $ \geq$  or > is used, shade above the line and the symbol $\leq$ or < is used shade below the line.

Note: Students can go wrong by confusing with meaning of the sign of inequalities it’s important to remember the symbol $\geq$ or > is used, shade above the line and the symbol $\leq$ or < is used shade below the line.