Question

What is the lateral displacement when a ray of light falls normally on a glass slab?

Answer 1

- Hint: Use Snell’s law i.e. ${{\mu }_{1}}\sin i={{\mu }_{2}}\sin r$ , where $i$ is the angle of incidence and $r$ is the angle of refraction at the interface of the two mediums. ${{\mu }_{1}}$ is the refractive index of the medium where the light is incident and ${{\mu }_{2}}$ is the refractive index of the medium where the light gets refracted.

Complete step-by-step solution -

 A glass slab is in cuboidal shape (opposite surfaces parallel to each other). Let us first understand what happens when a light ray enters a glass slab. When a light ray passes through a glass slab it is refracted twice at the two parallel faces and finally emerges parallel to its incident direction. Suppose a light ray enters the glass slab from air. It will first be refracted at this surface.

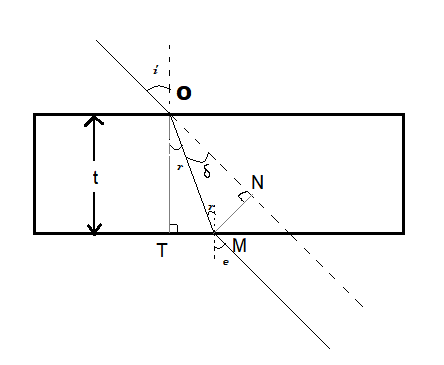
Use Snell’s law i.e. ${{\mu }_{1}}\sin i={{\mu }_{2}}\sin r$.
$\Rightarrow 1.\sin i=(1.5).\sin r$ …….(1) (Refractive indices of air and glass are 1 and 1.5 respectively)
Afterwards, the refracted ray will travel through the glass and will be incident on the opposite surface. Here, as you can see in the given figure, the angle of incident at surface 2 will be equal to the angle of refraction at surface 1 (since the normal at the two surfaces are parallel).
Let the angle of refraction at surface two be ‘e’. Now, use Snell’s law.
$\Rightarrow 1.\sin e=(1.5)\sin r$ …….(2)
Compare equations (1) and (2). We get, $i=e$. Hence, the emergent ray is parallel to the incident ray. The distance between these two rays is called the lateral displacement. Now, let us find an expression for the lateral displacement. For that, let the thickness of the glass slab be ‘t’.
As you can see in the given figure, $\vartriangle OMN$ is a right-angled triangle where MN is the lateral displacement. We have an expression for MN. In $\vartriangle OTM$ , $\sin \delta =\dfrac{MN}{OM}$
$\Rightarrow MN=OM\sin \delta $ ….(3).
In $\vartriangle OTM$ , $\cos r=\dfrac{OT}{OM}=\dfrac{t}{OM}$
$\Rightarrow OM=t\sec r$ ……(4).
Substitute the value of OM from equation (4) into equation (3).
$\Rightarrow MN=t\sec r.\sin \delta $ And $\delta =i-r$
$\Rightarrow MN=t\sec r.\sin \left( i-r \right)$
Therefore, we got the expression for lateral displacement. Now, if the light ray is incident normally on the surface, $i=0$. Hence, $r=0$. Therefore, MN will be zero. Meaning there will be any displacement in the ray of light.

Note: When a light ray falls on a glass slab, it is not that there will be a lateral displacement every time. One example you saw in the question. Another example is the internal reflection of the ray. The ray does refract into the outside medium, but it is reflected back into the same medium. This is only when the ray travels from a denser medium to a rarer medium.