Question

What is lateral shift? Explain the relationship between focal length and radius of curvature of a mirror.

Answer 1

- Hint: A shift signifies a deviation from its usual path. When we consider light its shift in the path taken by the light. You can use snell's law and some basic geometry to determine how much is the shift. To determine the relationship between focal length and radius of curvature of a mirror, draw the ray diagram of a concave mirror and determine the relationship using geometry.

Complete step-by-step solution -

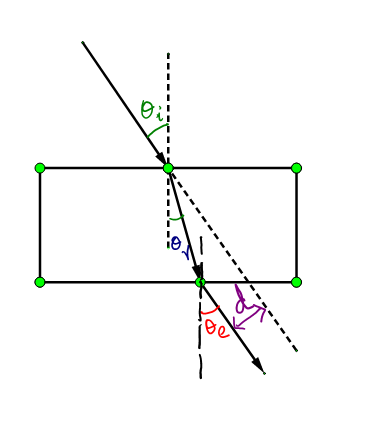
So in order to understand the lateral shift, consider a denser medium bounded by a non- denser medium, for example, a glass slab placed in the air, which is made up of glass which has a higher refractive index higher than air. So when a light ray enters the glass slab from the air at an angle ${{\theta }_{i}}$, refraction takes place and the light ray inside the glass slab bends toward the normal forming an angle ${{\theta }_{r}}$with the normal. This refracted light ray when it reaches the end of the glass slab refracts again and the light bends away from the normal. We can see there is a shift in the direction of the incident ray and emergent ray. The perpendicular distance between the incident and emergent ray is known as the lateral shift. In the figure, it is denoted by ‘d’.

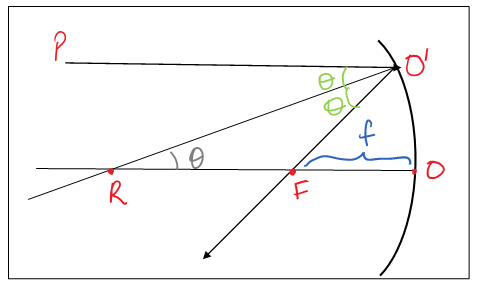
Consider a concave mirror with a radius of curvature at ‘R’, focus at ‘F’ and center at ‘O’. Suppose a light ray PO’ hits the surface of a mirror at O’ (O’=O, since we are considering a thin mirror). After reflection the light ray goes through F, a normal is drawn from O’ which passes through R. From the constructions we have,
$\angle PO'R=\angle RO'F=\theta $ (law of reflection) …. Equation (1)
Also $\angle O'RF=\theta $ (Alternate angles) ……..Equation (2)
From equation (1) and (2), we get
$\angle RO'F=\angle O'RF$
$\therefore \Delta O'FR$ is an isosceles triangle, with sides O’F=FR.
Since we are considering a thin mirror O’F=OF. Therefore OF=FR….. equation (3)
OF is the focal length ‘f’ of the mirror and ‘R’ is the radius of curvature.
From the figure it is clear that the radius of curvature R=OF+FR. From equation (3) we get,
$\begin{align}
  & \text{R}=\text{OF}+\text{FR} \\
 & \text{R}=\text{f}+\text{f} \\
\end{align}$
$\text{R}=\text{2f}$
Where, f is the focal length and R is the radius of curvature of the mirror.

Note: Concave mirrors usually give real and inverted images except when the object is placed at the focus of the mirror, so the image formed will be virtual.
Convex mirrors usually form a virtual image of the object.