
Length of the normal chord of the parabola
A.13
B.8
C.
D.4
Answer
517.2k+ views
Hint: Take the focal chord as PQ. Their coordinates are of the form
Complete step-by-step answer:
We have been given the equation of parabola as
First let us draw the parabola
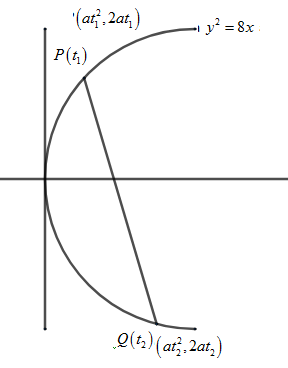
We know the general equation of a parabola as
From that we get, latus rectum
Let us take the two points on the parabola as
Similarly we know that
It is said that the abscissa and ordinates are equal, the coordinates are equal so put y=x.
So,
i.e. x can be either 0 or 8. So when x=8, y=8
Thus we got the coordinate of
We can take the coordinate of
Thus we got a=2, So,
Now we get the coordinate of
Now let us equate the x and y coordinates of both.
Thus,
Thus we got
We know that
Thus
Thus let us put
Now, let us find the length of normal chord PQ using distance formula
distance
Put
Length of normal chord PQ
Hence we got the length of a normal chord as
Therefore, option (C) is the correct answer.
Note: The normal at the point
Complete step-by-step answer:
We have been given the equation of parabola as
First let us draw the parabola
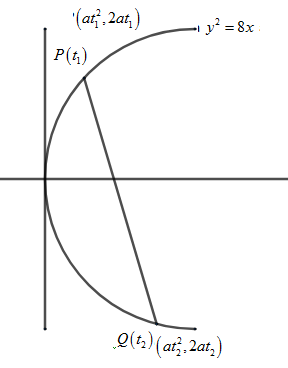
We know the general equation of a parabola as
From that we get, latus rectum
Let us take the two points on the parabola as
Similarly we know that
It is said that the abscissa and ordinates are equal, the coordinates are equal so put y=x.
So,
i.e. x can be either 0 or 8. So when x=8, y=8
Thus we got the coordinate of
We can take the coordinate of
Thus we got a=2, So,
Now we get the coordinate of
Now let us equate the x and y coordinates of both.
Thus,
Thus we got
We know that
Thus
Thus let us put
Now, let us find the length of normal chord PQ using distance formula
distance
Put
Length of normal chord PQ
Hence we got the length of a normal chord as
Therefore, option (C) is the correct answer.
Note: The normal at the point
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




