Question

Let $A$ and $B$ be two sets then ${\left( {A \cup B} \right)^\prime } \cup \left( {A' \cap B} \right)$ is equal to
1)$A'$
2)$A$
3)$B'$
4) None of these

Answer 1

Hint: First we will assume a universal set of the two sets $A$ and $B$. Then, by using the properties of set theory we can deduce the given parts of the required set, that is ${\left( {A \cup B} \right)^\prime }$ and \[\left( {A' \cap B} \right)\]. By deducing the solutions of these two parts by properties of sets, we can find the union of the two sets and can further reduce or simplify that as required. We will use De Morgan’s laws for simplification of the set's operations.

Complete answer: Let a universal set of $A$ and $B$ be $U$.
Now, the required set is ${\left( {A \cup B} \right)^\prime } \cup \left( {A' \cap B} \right)$.
From the first part of the required set, we have, ${\left( {A \cup B} \right)^\prime }$.
Now, we know the De Morgan’s law of set theory as ${\left( {A \cup B} \right)^\prime } = \left( {{A^\prime } \cap {B^\prime }} \right)$
So, we substitute the value of ${\left( {A \cup B} \right)^\prime }$ as $\left( {{A^\prime } \cap {B^\prime }} \right)$ in the expression. So, we get,
\[ \Rightarrow \left( {{A^\prime } \cap {B^\prime }} \right) \cup \left( {A' \cap B} \right)\]
Now, taking the common terms outside the bracket, we get,
\[ \Rightarrow {A^\prime } \cap \left( {{B^\prime } \cup B} \right)\]
Now, we know that union of a set and its complement constitutes the universal set denoted by the symbol U. So, we get,
\[ \Rightarrow {A^\prime } \cap U\]
Now, we have to find the intersection of the complement of $A$ and the universal set.
Here, $A'$ is the set excluding $A$ from the universal set $U$. So, the complement of A and the universal set have the complement of A as the common region.
So, the value of the expression is,
\[ \Rightarrow {A^\prime } \cap U = A'\]
Therefore option (1) is the correct answer.

Note:
We should have a clear understanding of the concepts of set theory. We must know the meaning of complement of a set, union and intersection of two sets. One should remember De Morgan’s laws of set theory in order to get to the final answer of the given problem. We can also solve the given problem using Venn diagrams.
So, we have, ${\left( {A \cup B} \right)^\prime } \cup \left( {A' \cap B} \right)$
We know that $\left( {A \cup B} \right)$ is depicted as follows:

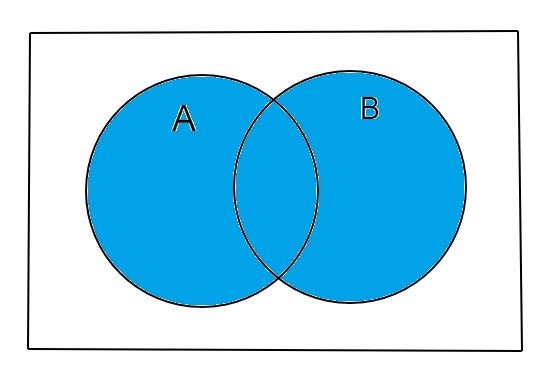
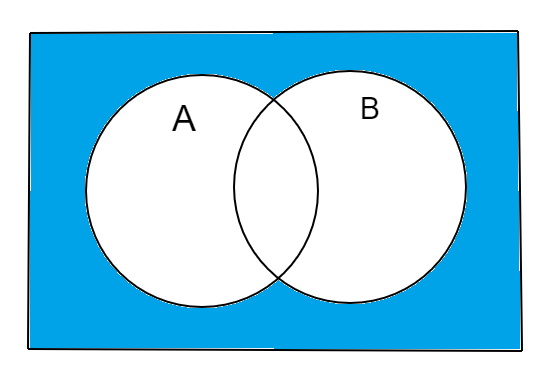
So, complement of $\left( {A \cup B} \right)$ is depicted as follows:

Also, we know that $\left( {A' \cap B} \right)$ can be resented as:

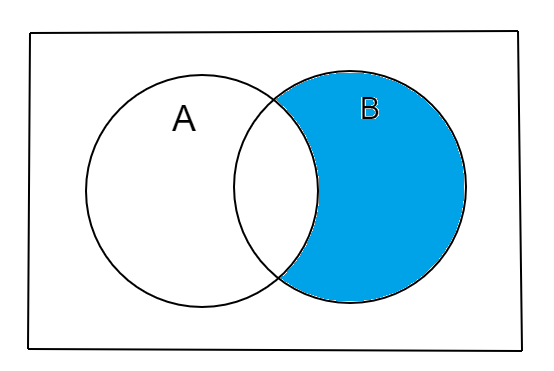
So, the union of the two set expressions $\left( {A' \cap B} \right)$ and ${\left( {A \cup B} \right)^\prime }$ can be represented as Venn diagram as:

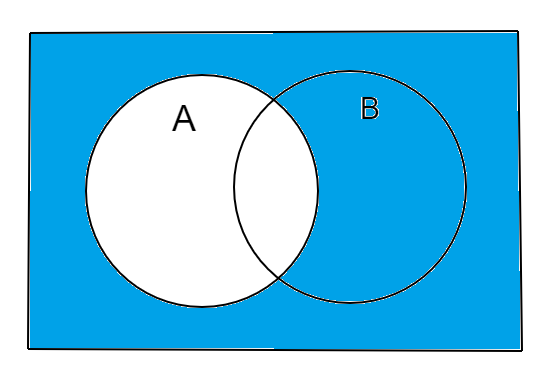
We know that the above Venn diagram is the equivalent of the complement of set A. Hence, the answer is $A'$.