
Let $ g\left( x \right)=ax+b $ , where $ a<0 $ and $ g $ is defined from $ \left[ 1,3 \right] $ onto $ \left[ 0,2 \right] $ then the value of $ {{\cot }^{-1}}\left( {{\cos }^{-1}}\left( \left| \sin x \right|+\left| \cos x \right| \right)+{{\sin }^{-1}}\left( -\left| \sin x \right|-\left| \cos x \right| \right) \right) $ is equal to \[\]
A. $ g\left( 1 \right) $ \[\]
B. $ g\left( 2 \right) $ \[\]
C. $ g\left( 3 \right) $ \[\]
D. $ g\left( 1 \right)+g\left( 3 \right) $ \[\]
Answer
569.4k+ views
Hint: We find the range of the function in the innermost bracket $ \left| \sin x \right|+\left| \cos x \right| $ using by taking $ y=\left| \sin x \right|+\left| \cos x \right| $ and then squaring and simplifying. We use symmetry to find the range of $ -\left| \sin x \right|-\left| \cos x \right|=-\left( \left| \sin x \right|+\left| \cos x \right| \right) $ . We find for what values of that range $ {{\cos }^{-1}}x,{{\sin }^{-1}}x $ are well defined and then find $ {{\cot }^{-1}}x $ at those values. We find the function $ g\left( x \right)=ax+b $ g to be linear decreasing function and compare for what values of $ x $ $ g\left( x \right)={{\cot }^{-1}}x $ .\[\]
Complete step by step answer:
Let us first find the value of inverse cotangent function in the given in the question as a composites function. We have;
\[{{\cot }^{-1}}\left( {{\cos }^{-1}}\left( \left| \sin x \right|+\left| \cos x \right| \right)+{{\sin }^{-1}}\left( -\left| \sin x \right|-\left| \cos x \right| \right) \right)\]
We know that inverse cosine function $ {{\cos }^{-1}}x $ and inverse sine function $ {{\sin }^{-1}}x $ can take values only from the interval $ \left[ -1,1 \right] $ since they are defined as $ {{\cos }^{-1}}x:\left[ -1,1 \right]\to \left[ 0,\pi \right] $ and $ {{\sin }^{-1}}x:\left[ -1,1 \right]\to \left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right] $ .\[\]
We see that $ {{\cos }^{-1}}x $ has the argument $ \left| \sin x \right|+\left| \cos x \right| $ and $ {{\sin }^{-1}}x $ has the argument $ -\left| \sin x \right|-\left| \cos x \right|=-\left( \left| \sin x \right|+\left| \cos x \right| \right) $ . Let us find the range of $ \left| \sin x \right|+\left| \cos x \right| $ . Let us assume.
\[y=\left| \sin x \right|+\left| \cos x \right|\]
We square both side and use the algebraic identity $ {{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab $ to have;
\[\Rightarrow {{y}^{2}}={{\left| \sin x \right|}^{2}}+{{\left| \cos x \right|}^{2}}+2\left| \sin x \right|\left| \cos x \right|\]
We use the property of modulus $ \left| a \right|\left| b \right|=\left| ab \right| $ for $ a=\sin x,b=\cos x $ in the above step to have
\[\Rightarrow {{y}^{2}}={{\sin }^{2}}x+{{\cos }^{2}}x+2\left| \sin x\cos x \right|\]
We use Pythagorean trigonometric identity $ {{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1 $ and the sine double angle formula $ \sin 2\theta =2\sin \theta \cos \theta $ for $ \theta =x $ in the above step to have;
\[\Rightarrow {{y}^{2}}=1+\left| \sin 2x \right|\]
We take square root both side and have ;
\[\Rightarrow y=\sqrt{1+\left| \sin 2x \right|}\]
We know the $ \sin \theta $ lies in between $ -1 $ to 1 for all real values of $ \theta . $ So for $ \theta =2x $ we have;
\[\begin{align}
& -1\le \sin 2x\le 1 \\
& \Rightarrow 0\le \left| \sin 2x \right|\le 1 \\
& \Rightarrow 1\le 1+\left| \sin 2x \right|\le 1+1 \\
& \Rightarrow 1\le 1+\left| \sin 2x \right|\le 2 \\
\end{align}\]
We take square roots in all the terms to have;
\[\begin{align}
& \Rightarrow 1\le \sqrt{1+\left| \sin 2x \right|}\le \sqrt{2} \\
& \Rightarrow 1\le y\le \sqrt{2} \\
& \Rightarrow 1\le \left| \sin x \right|+\left| \cos x \right|\le \sqrt{2} \\
\end{align}\]
So we have $ \left| \sin x \right|+\left| \cos x \right|\in \left[ 1,\sqrt{2} \right] $ . We use the property of symmetric property of functions about $ x- $ axis and conclude that $ -\left( \left| \sin x \right|+\left| \cos x \right| \right)\in \left[ -\sqrt{2},-1 \right] $ . Now see that only value $ {{\cos }^{-1}}x $ can take from $ \left| \sin x \right|+\left| \cos x \right|\in \left[ 1,\sqrt{2} \right] $ is 1 since the maximum value that $ {{\cos }^{-1}}x $ c can take is 1 and the only value $ {{\sin }^{-1}}x $ can take from $ -\left( \left| \sin x \right|+\left| \cos x \right| \right)\in \left[ -\sqrt{2},-1 \right] $ is $ -1 $ since the minimum value $ {{\sin }^{-1}}x $ can take is $ -1. $ So we have
\[\begin{align}
& \Rightarrow {{\cot }^{-1}}\left( {{\cos }^{-1}}\left( \left| \sin x \right|+\left| \cos x \right| \right)+{{\sin }^{-1}}\left( -\left| \sin x \right|-\left| \cos x \right| \right) \right) \\
& \Rightarrow {{\cot }^{-1}}\left( {{\cos }^{-1}}\left( 1 \right)+{{\sin }^{-1}}\left( -1 \right) \right) \\
& \Rightarrow {{\cot }^{-1}}\left( 0-\dfrac{\pi }{2} \right)={{\cot }^{-1}}\left( \dfrac{-\pi }{2} \right)=0....\left( 1 \right) \\
\end{align}\]
We are given t $ g\left( x \right)=ax+b $ , where $ a<0 $ and $ g $ is defined from $ \left[ 1,3 \right] $ onto $ \left[ 0,2 \right] $ and are asked for what values of $ x $ ,
\[\Rightarrow {{\cot }^{-1}}\left( {{\cos }^{-1}}\left( \left| \sin x \right|+\left| \cos x \right| \right)+{{\sin }^{-1}}\left( -\left| \sin x \right|-\left| \cos x \right| \right) \right)=g\left( x \right)\]
Since the value of inverse cotangent function is 0 for all $ x $ as obtained in (1) we have;
\[\begin{align}
& \Rightarrow 0=g\left( x \right) \\
& \Rightarrow g\left( x \right)=0 \\
\end{align}\]
We now need to find the $ x $ for which $ g\left( x \right)=0 $ . We see that $ g\left( x \right)=ax+b $ is a linear function with an equation of line with negative slope $ \left( \because a<0 \right) $ and hence the function $ g\left( x \right) $ is decreasing. So $ g $ maps the endpoints of the intervals $ \left[ 1,3 \right] $ oppositely to the endpoints of $ \left[ 0,2 \right] $ which means $ g\left( 1 \right)=2 $ and $ g\left( 3 \right)=0 $ . So the correct option is C. \[\]
Note:
We note that the range and domain of inverse co-tangent function is given respectively as $ \mathsf{\mathbb{R}} $ and $ \left( 0,\pi \right) $ and hence here $ {{\cot }^{-1}}\left( \dfrac{-\pi }{2} \right) $ is well defined.\[\]
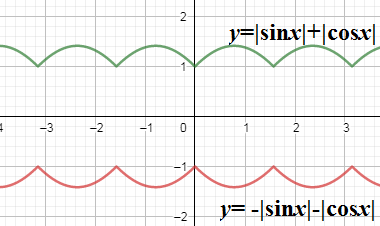
We also note that the plot of two functions $ y=f\left( x \right) $ and $ y=-f\left( x \right) $ will always be symmetrical about $ x- $ axis and the plot of the functions $ y=f\left( x \right),y=f\left( -x \right) $ will always be symmetrical about $ y- $ axis provided $ f\left( x \right) $ is not even.
Complete step by step answer:
Let us first find the value of inverse cotangent function in the given in the question as a composites function. We have;
\[{{\cot }^{-1}}\left( {{\cos }^{-1}}\left( \left| \sin x \right|+\left| \cos x \right| \right)+{{\sin }^{-1}}\left( -\left| \sin x \right|-\left| \cos x \right| \right) \right)\]
We know that inverse cosine function $ {{\cos }^{-1}}x $ and inverse sine function $ {{\sin }^{-1}}x $ can take values only from the interval $ \left[ -1,1 \right] $ since they are defined as $ {{\cos }^{-1}}x:\left[ -1,1 \right]\to \left[ 0,\pi \right] $ and $ {{\sin }^{-1}}x:\left[ -1,1 \right]\to \left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right] $ .\[\]
We see that $ {{\cos }^{-1}}x $ has the argument $ \left| \sin x \right|+\left| \cos x \right| $ and $ {{\sin }^{-1}}x $ has the argument $ -\left| \sin x \right|-\left| \cos x \right|=-\left( \left| \sin x \right|+\left| \cos x \right| \right) $ . Let us find the range of $ \left| \sin x \right|+\left| \cos x \right| $ . Let us assume.
\[y=\left| \sin x \right|+\left| \cos x \right|\]
We square both side and use the algebraic identity $ {{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab $ to have;
\[\Rightarrow {{y}^{2}}={{\left| \sin x \right|}^{2}}+{{\left| \cos x \right|}^{2}}+2\left| \sin x \right|\left| \cos x \right|\]
We use the property of modulus $ \left| a \right|\left| b \right|=\left| ab \right| $ for $ a=\sin x,b=\cos x $ in the above step to have
\[\Rightarrow {{y}^{2}}={{\sin }^{2}}x+{{\cos }^{2}}x+2\left| \sin x\cos x \right|\]
We use Pythagorean trigonometric identity $ {{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1 $ and the sine double angle formula $ \sin 2\theta =2\sin \theta \cos \theta $ for $ \theta =x $ in the above step to have;
\[\Rightarrow {{y}^{2}}=1+\left| \sin 2x \right|\]
We take square root both side and have ;
\[\Rightarrow y=\sqrt{1+\left| \sin 2x \right|}\]
We know the $ \sin \theta $ lies in between $ -1 $ to 1 for all real values of $ \theta . $ So for $ \theta =2x $ we have;
\[\begin{align}
& -1\le \sin 2x\le 1 \\
& \Rightarrow 0\le \left| \sin 2x \right|\le 1 \\
& \Rightarrow 1\le 1+\left| \sin 2x \right|\le 1+1 \\
& \Rightarrow 1\le 1+\left| \sin 2x \right|\le 2 \\
\end{align}\]
We take square roots in all the terms to have;
\[\begin{align}
& \Rightarrow 1\le \sqrt{1+\left| \sin 2x \right|}\le \sqrt{2} \\
& \Rightarrow 1\le y\le \sqrt{2} \\
& \Rightarrow 1\le \left| \sin x \right|+\left| \cos x \right|\le \sqrt{2} \\
\end{align}\]
So we have $ \left| \sin x \right|+\left| \cos x \right|\in \left[ 1,\sqrt{2} \right] $ . We use the property of symmetric property of functions about $ x- $ axis and conclude that $ -\left( \left| \sin x \right|+\left| \cos x \right| \right)\in \left[ -\sqrt{2},-1 \right] $ . Now see that only value $ {{\cos }^{-1}}x $ can take from $ \left| \sin x \right|+\left| \cos x \right|\in \left[ 1,\sqrt{2} \right] $ is 1 since the maximum value that $ {{\cos }^{-1}}x $ c can take is 1 and the only value $ {{\sin }^{-1}}x $ can take from $ -\left( \left| \sin x \right|+\left| \cos x \right| \right)\in \left[ -\sqrt{2},-1 \right] $ is $ -1 $ since the minimum value $ {{\sin }^{-1}}x $ can take is $ -1. $ So we have
\[\begin{align}
& \Rightarrow {{\cot }^{-1}}\left( {{\cos }^{-1}}\left( \left| \sin x \right|+\left| \cos x \right| \right)+{{\sin }^{-1}}\left( -\left| \sin x \right|-\left| \cos x \right| \right) \right) \\
& \Rightarrow {{\cot }^{-1}}\left( {{\cos }^{-1}}\left( 1 \right)+{{\sin }^{-1}}\left( -1 \right) \right) \\
& \Rightarrow {{\cot }^{-1}}\left( 0-\dfrac{\pi }{2} \right)={{\cot }^{-1}}\left( \dfrac{-\pi }{2} \right)=0....\left( 1 \right) \\
\end{align}\]
We are given t $ g\left( x \right)=ax+b $ , where $ a<0 $ and $ g $ is defined from $ \left[ 1,3 \right] $ onto $ \left[ 0,2 \right] $ and are asked for what values of $ x $ ,
\[\Rightarrow {{\cot }^{-1}}\left( {{\cos }^{-1}}\left( \left| \sin x \right|+\left| \cos x \right| \right)+{{\sin }^{-1}}\left( -\left| \sin x \right|-\left| \cos x \right| \right) \right)=g\left( x \right)\]
Since the value of inverse cotangent function is 0 for all $ x $ as obtained in (1) we have;
\[\begin{align}
& \Rightarrow 0=g\left( x \right) \\
& \Rightarrow g\left( x \right)=0 \\
\end{align}\]
We now need to find the $ x $ for which $ g\left( x \right)=0 $ . We see that $ g\left( x \right)=ax+b $ is a linear function with an equation of line with negative slope $ \left( \because a<0 \right) $ and hence the function $ g\left( x \right) $ is decreasing. So $ g $ maps the endpoints of the intervals $ \left[ 1,3 \right] $ oppositely to the endpoints of $ \left[ 0,2 \right] $ which means $ g\left( 1 \right)=2 $ and $ g\left( 3 \right)=0 $ . So the correct option is C. \[\]
Note:
We note that the range and domain of inverse co-tangent function is given respectively as $ \mathsf{\mathbb{R}} $ and $ \left( 0,\pi \right) $ and hence here $ {{\cot }^{-1}}\left( \dfrac{-\pi }{2} \right) $ is well defined.\[\]
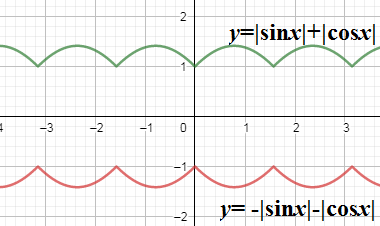
We also note that the plot of two functions $ y=f\left( x \right) $ and $ y=-f\left( x \right) $ will always be symmetrical about $ x- $ axis and the plot of the functions $ y=f\left( x \right),y=f\left( -x \right) $ will always be symmetrical about $ y- $ axis provided $ f\left( x \right) $ is not even.
Recently Updated Pages
Master Class 10 Computer Science: Engaging Questions & Answers for Success

Master Class 10 General Knowledge: Engaging Questions & Answers for Success

Master Class 10 English: Engaging Questions & Answers for Success

Master Class 10 Social Science: Engaging Questions & Answers for Success

Master Class 10 Maths: Engaging Questions & Answers for Success

Master Class 10 Science: Engaging Questions & Answers for Success

Trending doubts
What is the median of the first 10 natural numbers class 10 maths CBSE

Which women's tennis player has 24 Grand Slam singles titles?

Who is the Brand Ambassador of Incredible India?

Why is there a time difference of about 5 hours between class 10 social science CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

State and prove converse of BPT Basic Proportionality class 10 maths CBSE




