Question

Let S be the set of all real values of $\lambda$ such that a plane passing through the points $(-{\lambda }^2,1,1),(1,-{\lambda }^2,1)\text{ and }(1,1,-{\lambda }^2)$ also passes through the point (-1, -1, 1). Then S is equal to:
$$\begin{array}{rl}& A.\left(\sqrt{3}\right)\\ & B.(\sqrt{3}-\sqrt{3})\\ & C.(1,-1)\\ & D.(3,-3)\end{array}$$

Answer 1

Hint: Here, according to the question, all four points are lying on the plane. Suppose, we have a plane as shown below:

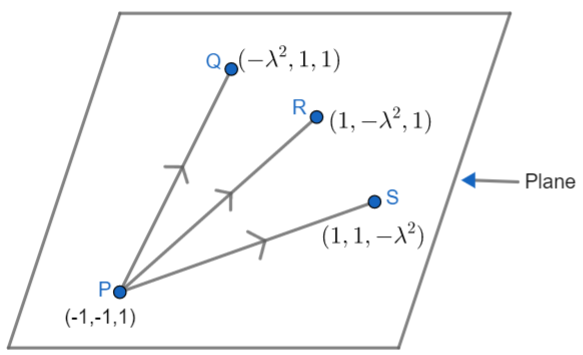
Let P, Q, R, S be the points on the plane. So, first we have to find the position vectors of each point as PQ, PR, PS by subtracting the coordinates of corresponding points. Since they are all collinear points, we will apply the condition for collinearity, i.e the determinant of these position vectors will be 0. We can express it as
We know that, if
$$\begin{array}{rl}& (x_1\hat{i}+y_1\hat{j}+z_1\hat{k})\\ & (x_2\hat{i}+y_2\hat{j}+z_2\hat{k})\\ & (x_3\hat{i}+y_3\hat{j}+z_3\hat{k})\end{array}\}\text{ are three coplanar vectors}$$
Then, the condition is $$\left|\begin{array}{ccc}{x}_1& y_1& z_1\\ x_2& y_2& z_2\\ x_3& y_3& z_3\end{array}\right|=0$$

Complete step by step answer:
Now, we have to start the solution. First step is to find the position vectors. If we have to find PQ, then we have to deduct the coordinates of point P from coordinates of point Q. Similar, we can do this for all the three position vector as shown below,
$$\begin{array}{rl}& \overrightarrow{PQ}=(-{\lambda }^2-(-1))\hat{i}+(1-(-1))\hat{j}+(1-1)\hat{k}\\ & \Rightarrow (1-{\lambda }^2)\hat{i}+2\hat{j}+0\hat{k}\\ & \overrightarrow{PR}=(1-(-1))\hat{i}+(-{\lambda }^2-(-1))\hat{j}+(1-1)\hat{k}\\ & \Rightarrow 2\hat{i}+(1-{\lambda }^2)\hat{j}+0\hat{k}\\ & \overrightarrow{PS}=(1-(-1))\hat{i}+(1-(-1))\hat{j}+(-{\lambda }^2-1)\hat{k}\\ & \Rightarrow 2\hat{i}+2\hat{j}+(-{\lambda }^2-1)\hat{k}\end{array}$$
Here, $\overrightarrow{PQ,}\overrightarrow{PR}\text{ and }\overrightarrow{PS}$ are three coplanar vectors.
We know that, if
$$\begin{array}{rl}& (x_1\hat{i}+y_1\hat{j}+z_1\hat{k})\\ & (x_2\hat{i}+y_2\hat{j}+z_2\hat{k})\\ & (x_3\hat{i}+y_3\hat{j}+z_3\hat{k})\end{array}\}\text{ are three coplanar vectors}$$
Then, $$\left|\begin{array}{ccc}{x}_1& y_1& z_1\\ x_2& y_2& z_2\\ x_3& y_3& z_3\end{array}\right|=0$$
So, we can substitute the results obtained above and then evaluate the determinant and equate it to 0 as shown below,
$$\begin{array}{rl}& \left|\begin{array}{ccc}1-{\lambda }^2& 2& 0\\ 2& 1-{\lambda }^2& 0\\ 2& 2& -{\lambda }^2-1\end{array}\right|=0\\ & \Rightarrow (1-{\lambda }^2)\left[(1-{\lambda }^2)(-{\lambda }^2-1)\right]-2\left[2(-{\lambda }^2-1)\right]=0\\ & \Rightarrow ({\lambda }^2-1)\left[(1-{\lambda }^2)(1+{\lambda }^2)\right]+4(1+{\lambda }^2)=0\\ & \Rightarrow (1+{\lambda }^2)[4-{({\lambda }^2-1)}^2]=0\end{array}$$
We know $1+{\lambda }^2\ne 0$ therefore,
$$\begin{array}{rl}& {({\lambda }^2-1)}^2=4\\ & ({\lambda }^2-1)=\pm 2\end{array}$$
Now, as $({\lambda }^2-1)=\pm 2$ therefore,
$$\begin{array}{rl}& ({\lambda }^2-1)=-2\\ & {\lambda }^2=-1\end{array}\}\text{ Not possible}$$
Since it is an imaginary number.
$$\begin{array}{rl}& ({\lambda }^2-1)=2\\ & {\lambda }^2=3\\ & \lambda =\pm \sqrt{3}\end{array}\}\text{ Possible}$$

So, the correct answer is “Option B”.

Note: Here, we have taken P (-1, -1, 1) that doesn't mean this point should contain constant coordinates, we can take any other points as P (as the base point). Answer will be the same. We should also know the elementary idea of how to find the vector using two given points. Like here, for finding $\overrightarrow{PQ}$ subtract the coordinates of the point where the arrow is pointing from the coordinates of the point, where the arrow is originating.