
Let the equation of a circle and a parabola be
[a] (1,-1) is a point on the common chord of contact.
[b] The equation of the common chord is y+1=0
[c] The length of the common chord is 6
[d] None of these.
Answer
517.8k+ views
Hint:Draw a rough diagram of the curves. Find the coordinates of the points of intersection of these curves. Use the fact that the equation of the line passing through points
Complete step-by-step answer:
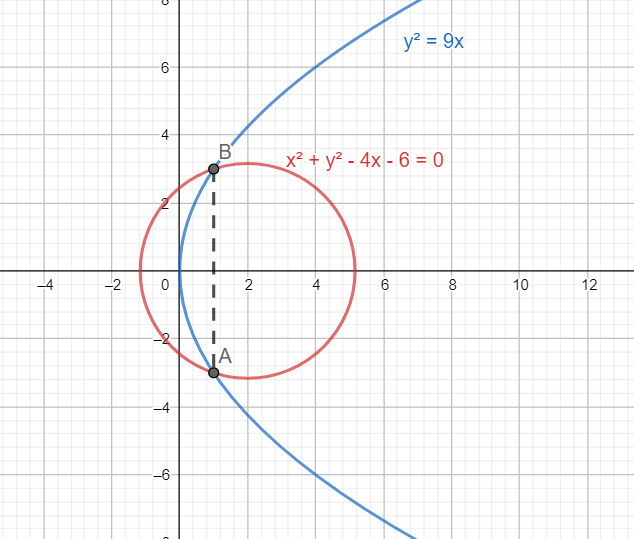
AB is the common chord.
Finding the coordinates of A and B:
A and B are the points of intersection of the curves
Hence we solve these equations simultaneously to get the coordinates of A and B.
Substituting the value of
We use the method of splitting the middle term to solve the quadratic equation.
We have 5 = 6-1 and
Hence, we have
Taking x common from the first two terms and -1 common from the last two terms, we get
Taking x+6 common from both the terms, we get
Using zero product property, we have
Hence, we have
Since from the equation of the parabola, we have
Hence, we have x= -6 is rejected.
Hence, we have x =1
When x= 1, we have
Hence, we have
Now, we know that the equation of the line passing through points
Hence, we have
Hence the equation fo the line AB is
Hence the equation of the line AB is x-1= 0
Hence option [b] is incorrect.
Clearly, the point (1,-1) lies on AB.
Hence option [a] is correct.
Now, we know that the distance between the points
Hence, we have
Hence, the length of the common chord is 6.
Hence option [c] is correct.
Hence options [a] and [c] are correct.
Note: [1] If using the equations of two second-degree curves, you can eliminate the quadratic terms, then the resulting equation is the equation of the common chord. In the above case, it was not possible. This, however, is possible in case of two ellipses or two circles, or a circle and an ellipse or two parabolas etc.
Complete step-by-step answer:

AB is the common chord.
Finding the coordinates of A and B:
A and B are the points of intersection of the curves
Hence we solve these equations simultaneously to get the coordinates of A and B.
Substituting the value of
We use the method of splitting the middle term to solve the quadratic equation.
We have 5 = 6-1 and
Hence, we have
Taking x common from the first two terms and -1 common from the last two terms, we get
Taking x+6 common from both the terms, we get
Using zero product property, we have
Hence, we have
Since from the equation of the parabola, we have
Hence, we have x= -6 is rejected.
Hence, we have x =1
When x= 1, we have
Hence, we have
Now, we know that the equation of the line passing through points
Hence, we have
Hence the equation fo the line AB is
Hence the equation of the line AB is x-1= 0
Hence option [b] is incorrect.
Clearly, the point (1,-1) lies on AB.
Hence option [a] is correct.
Now, we know that the distance between the points
Hence, we have
Hence, the length of the common chord is 6.
Hence option [c] is correct.
Hence options [a] and [c] are correct.
Note: [1] If using the equations of two second-degree curves, you can eliminate the quadratic terms, then the resulting equation is the equation of the common chord. In the above case, it was not possible. This, however, is possible in case of two ellipses or two circles, or a circle and an ellipse or two parabolas etc.
Recently Updated Pages
Basicity of sulphurous acid and sulphuric acid are

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 4 Maths: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE




