
Let the refractive index of a denser medium with respect to a rare medium be ${N_{12}}$ and its critical angle${\theta _C}$. At an angle of incidence $A$ when light is travelling from denser medium to rarer medium, a part of the light is reflected and the rest is refracted and the angle between reflected and refracted rays is $90^\circ $. Angle $A$ is given by:
(A) ${\tan ^{ - 1}}(\sin {\theta _C})$
(B) $\dfrac{1}{{{{\tan }^{ - 1}}(\sin {\theta _C})}}$
(C) $\dfrac{1}{{{{\cos }^{ - 1}}(\sin {\theta _C})}}$
(D) ${\cos ^{ - 1}}(\sin {\theta _C})$
Answer
217.8k+ views
Hint: To find the angle of incidence we have to learn about the total internal reflection and its condition and about the critical angle we should also have knowledge about the Snell’s law to relate the critical angle with the angle of refraction and incidence.
Complete step by step answer
Angle of incidence is defined as the angle between a ray incident on a surface and the line perpendicular to the surface at the point of incidence.
When a ray of light hits a smooth polished surface, the light ray bounces back, it is called the reflection. The angle at which it bounce back is known as the angle of reflection
When light waves move from one medium to another, there is a change in the direction of waves due to the obstacles, so they bend and continue to pass it is known as refraction. The angle at which it bends is known as angle of refraction.
The relation between the angle of incidence and angle of refraction is given by Snell’s law
Snell's law states that the ratio of the sines of the angles of incidence to angle of refraction is equivalent to the ratio of phase velocities in the two media, or to the reciprocal of the ratio of the refractive indices
$\dfrac{{\sin {\text{ i}}}}{{\sin {\text{ r}}}} = \dfrac{{{v_i}}}{{{v_r}}}{\text{ or }}\dfrac{{{\mu _r}}}{{{\mu _i}}}$
Where,
Sin i is the angle of incidence
Sin r is the angle of refraction
${\mu _i}$ is the refractive index of the incident medium
${\mu _r}$ is the refractive index of the refractive medium
This relationship between the angles of incidence and refraction and the refractive indices of the two media is known as Snell's Law.
The critical angle is the angle of incidence beyond which light rays passing through a denser medium to the surface of a less dense medium are no longer refracted but totally reflected.
The critical angle is given by
$\sin {\theta _c} = \dfrac{{{\mu _r}}}{{{\mu _i}}}$
Here $\sin {\theta _c}$ is the critical angle.
Hence here the total internal reflection takes place.
Given,
The refractive index of a denser medium with respect to a rare medium be ${N_{12}}$
The critical angle is ${\theta _C}$
The angle between refracted and reflected ray is $90^\circ $
The angle of incidence is A
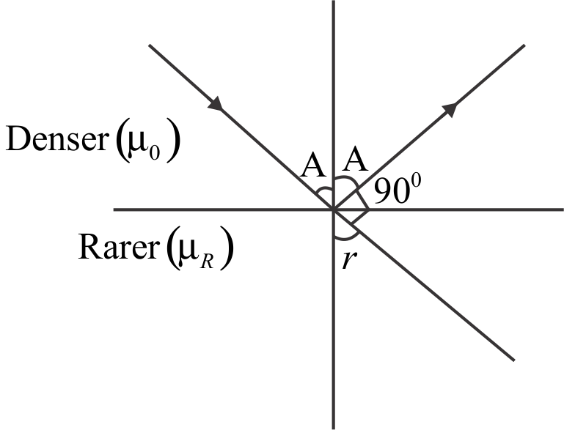
From the diagram
The angle of refraction is $90^\circ - A$
Critical angle is $\sin {\theta _c} = \dfrac{{{\mu _r}}}{{{\mu _i}}}$
We have seen that $\dfrac{{\sin {\text{ i}}}}{{\sin {\text{ r}}}} = \dfrac{{{\mu _r}}}{{{\mu _i}}}$
The critical angle becomes
$ \Rightarrow \sin {\theta _c} = \dfrac{{\sin {\text{ i}}}}{{\sin {\text{ r}}}}$
Substitute the known values
$ \Rightarrow \sin {\theta _c} = \dfrac{{\sin {\text{ A}}}}{{\sin {\text{ (90}}^\circ {\text{ - A)}}}}$
$ \Rightarrow \sin {\theta _c} = \dfrac{{\sin {\text{ A}}}}{{\cos {\text{ A}}}}$
$ \Rightarrow \sin {\theta _c} = \tan A$
$ \Rightarrow A = {\tan ^{ - 1}}\sin {\theta _c}$
Hence the correct answer is option (A) ${\tan ^{ - 1}}\sin {\theta _c}$
Note In the diagram we have noted an angle as A other than the incident angle it is the angle of reflection. The angle of reflection is also A because the angle of reflection is equal to the angle of incidence in total internal reflection.
Complete step by step answer
Angle of incidence is defined as the angle between a ray incident on a surface and the line perpendicular to the surface at the point of incidence.
When a ray of light hits a smooth polished surface, the light ray bounces back, it is called the reflection. The angle at which it bounce back is known as the angle of reflection
When light waves move from one medium to another, there is a change in the direction of waves due to the obstacles, so they bend and continue to pass it is known as refraction. The angle at which it bends is known as angle of refraction.
The relation between the angle of incidence and angle of refraction is given by Snell’s law
Snell's law states that the ratio of the sines of the angles of incidence to angle of refraction is equivalent to the ratio of phase velocities in the two media, or to the reciprocal of the ratio of the refractive indices
$\dfrac{{\sin {\text{ i}}}}{{\sin {\text{ r}}}} = \dfrac{{{v_i}}}{{{v_r}}}{\text{ or }}\dfrac{{{\mu _r}}}{{{\mu _i}}}$
Where,
Sin i is the angle of incidence
Sin r is the angle of refraction
${\mu _i}$ is the refractive index of the incident medium
${\mu _r}$ is the refractive index of the refractive medium
This relationship between the angles of incidence and refraction and the refractive indices of the two media is known as Snell's Law.
The critical angle is the angle of incidence beyond which light rays passing through a denser medium to the surface of a less dense medium are no longer refracted but totally reflected.
The critical angle is given by
$\sin {\theta _c} = \dfrac{{{\mu _r}}}{{{\mu _i}}}$
Here $\sin {\theta _c}$ is the critical angle.
Hence here the total internal reflection takes place.
Given,
The refractive index of a denser medium with respect to a rare medium be ${N_{12}}$
The critical angle is ${\theta _C}$
The angle between refracted and reflected ray is $90^\circ $
The angle of incidence is A

From the diagram
The angle of refraction is $90^\circ - A$
Critical angle is $\sin {\theta _c} = \dfrac{{{\mu _r}}}{{{\mu _i}}}$
We have seen that $\dfrac{{\sin {\text{ i}}}}{{\sin {\text{ r}}}} = \dfrac{{{\mu _r}}}{{{\mu _i}}}$
The critical angle becomes
$ \Rightarrow \sin {\theta _c} = \dfrac{{\sin {\text{ i}}}}{{\sin {\text{ r}}}}$
Substitute the known values
$ \Rightarrow \sin {\theta _c} = \dfrac{{\sin {\text{ A}}}}{{\sin {\text{ (90}}^\circ {\text{ - A)}}}}$
$ \Rightarrow \sin {\theta _c} = \dfrac{{\sin {\text{ A}}}}{{\cos {\text{ A}}}}$
$ \Rightarrow \sin {\theta _c} = \tan A$
$ \Rightarrow A = {\tan ^{ - 1}}\sin {\theta _c}$
Hence the correct answer is option (A) ${\tan ^{ - 1}}\sin {\theta _c}$
Note In the diagram we have noted an angle as A other than the incident angle it is the angle of reflection. The angle of reflection is also A because the angle of reflection is equal to the angle of incidence in total internal reflection.
Recently Updated Pages
Apparent Frequency Explained: Formula, Uses & Examples

Calorimetry: Definition, Principles & Calculations

Centrifugal Force Explained: Definition, Formula & Examples

Charge in a Magnetic Field: Definition, Formula & Examples

Charging and Discharging of a Capacitor Explained Simply

Combination of Capacitors: Series and Parallel Explained

Trending doubts
JEE Main 2026: Application Form Open, Exam Dates, Syllabus, Eligibility & Question Papers

Derivation of Equation of Trajectory Explained for Students

Hybridisation in Chemistry – Concept, Types & Applications

Understanding the Angle of Deviation in a Prism

Understanding Collisions: Types and Examples for Students

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Understanding Atomic Structure for Beginners

Ideal and Non-Ideal Solutions Explained for Class 12 Chemistry

Degree of Dissociation: Meaning, Formula, Calculation & Uses

Understanding Electromagnetic Waves and Their Importance

Understanding the Electric Field of a Uniformly Charged Ring




