Question

How to make the parabola of $y = {x^2} - 4x$.

Answer 1

Hint- In order to draw the graph of given parabola equation first we have to find the vertex of parabola which can be calculated by using the formula as vertex \[(aos,f(aos))\] so we will calculate \[aos\] in the solution further we will find intercept points of given parabola and by getting it we will plot the graph.

Complete step-by-step solution -
Given equation of parabola is $y = {x^2} - 4x $
At first we will calculate its vertex
As we know that if parabola equation is given as
$y = a{x^2} + bx + c$
Then axis of symmetry can be calculated by
$x = \dfrac{{ - b}}{{2a}}$
And vertex of given parabola equation is given as
Vertex \[(aos,f(aos))\]
Where \[c{\text{ }} = {\text{ }}y\] intercept
But here our function is
$y = {x^2} - 4x$
By comparing the given equation with general equation we have
$a = 1$
$b = - 4$
and $c = 0$
Therefore , axis of symmetry =
$x = \dfrac{{ - b}}{{2a}} = \dfrac{{ - ( - 4)}}{{2 \times 1}} = \dfrac{4}{2} = 2$
\[f(aos)\] means we put the \[aos\] back in our function as \[x\] and solve for $y$:
$ f(aos) = {(2)^2} - 4(2) \\
  f(aos) = 4 - 8 \\
  f(aos) = - 4 \\ $
Now vertex will be expressed as
Vertex = $(2, - 4)$
Now we will proceed further by calculating the intercept points of \[x\] axis and $y$ axis
For $y$ intercept we have to put the value of \[x\] as 0
So , at $x = 0$,
$ \because y = {x^2} - 4x \\
  y = {(0)^2} - 4(0) \\
  y = 0 \\ $
$y$ intercept $(0,0)$
Similarly , For \[x\] intercept we have to put the value of $y$ as 0
So, at \[y = 0\] ,
\[ \because y = {x^2} - 2x \\
  0 = {x^2} - 4x \\
  {x^2} - 4x = 0 \\
  x(x - 4) = 0 \\
  x = 0{\text{ and }}x = 4 \\ \]
By simplifying above equation we get two values of \[x\] as
\[x{\text{ }} = {\text{ }}0{\text{ }} and {\text{ }}x{\text{ }} = {\text{ }}4\]
Therefore, \[x\] intercept are $(0,0)$ and $(4,0)$
Now with the help of obtained data we will draw parabola of given equation
Vertex = $(2, - 4)$
\[x\] intercepts are $(0,0)$ and $(4,0)$
$y$ intercept $(0,0)$
 

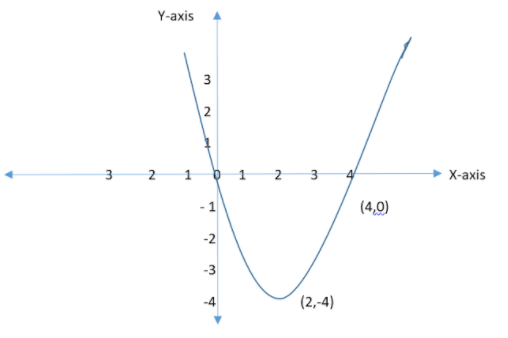
Note- The axis of symmetry of a parabola is a vertical line that divides the parabola into two congruent halves. The x-coordinate of the vertex is the equation of the axis of symmetry of the parabola. For a quadratic function in standard form, $y = a{x^2} + bx + c$ , the axis of symmetry is a vertical line $x = \dfrac{{ - b}}{{2a}}$ .