
What is meant by voids in crystal structure?
Answer
479.7k+ views
Hint: We know that Packing of atoms or molecules in crystals several possible arrangements but the one in which maximum available space is occupied.
Complete answer:
We can classify the close packing arrangements into square packing and hexagonal packing.
In the hexagonal arrangement, occupied space is
In square packing, arrangement of occupied space is
We have to remember that the arrangement of a solid sphere with close packing which remains some space is called voids.
-In three dimensions it shows interstitial sites in close packing of the sphere. Consider a triangular or trigonal site. Also of the above sites shows two different sites.
Now we discuss about the tetrahedral voids as,
-Tetrahedral sites: if three spheres are placed on the one spheres which are touching each other. Even four spheres touch one another some gaps available that know as the tetrahedral sites. In these sites, one sphere is surrounded by eight tetrahedral sites, and one site surrounded by four spheres. The coordination number is four and the ratio is
The diagram representation of tetrahedral voids is given as,
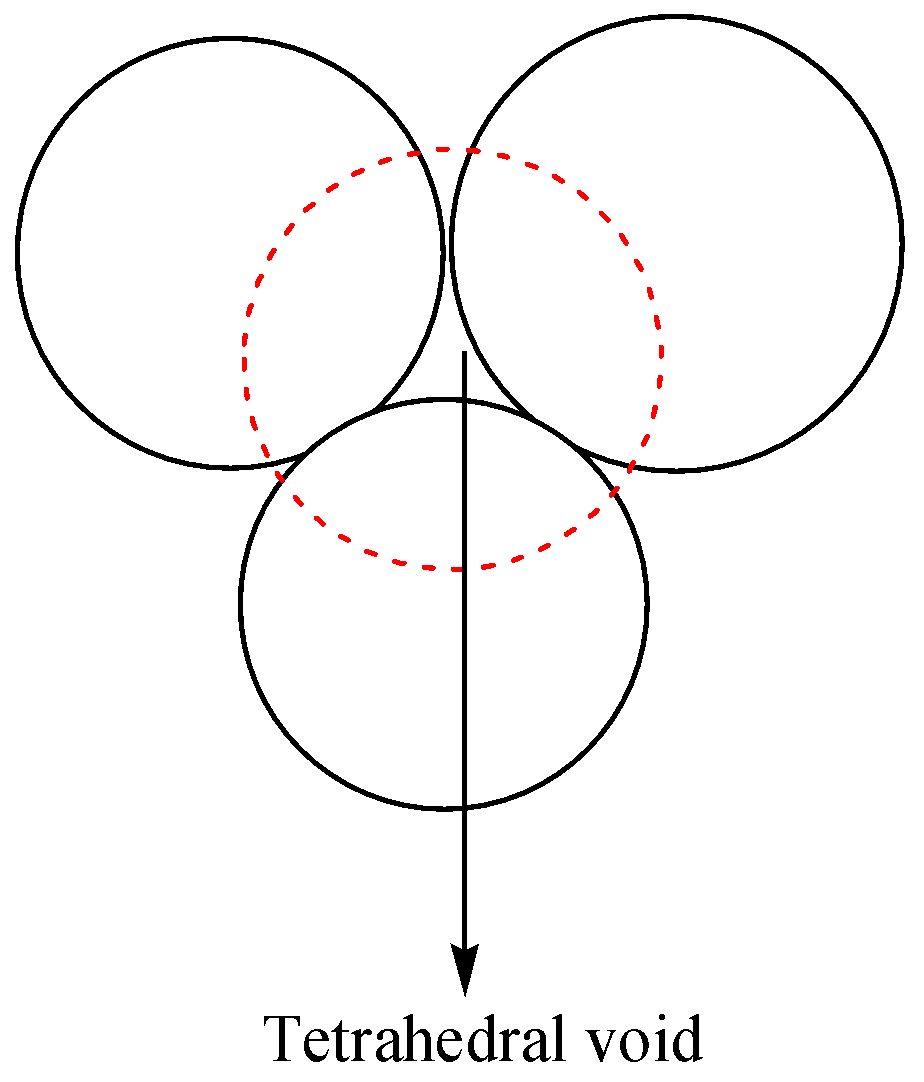
Now we discuss about the octahedral voids as,
Octahedral sites: The close packing of a sphere in hcp, as well as ccp arrangement, is known as octahedral sites. This shows six spheres attached in two forms. In these sites, one sphere is surrounded by six octahedral sites, and one site surrounded by six spheres. Hence the coordination number is six. Ratio is
The diagram representation of octahedral voids is given as,
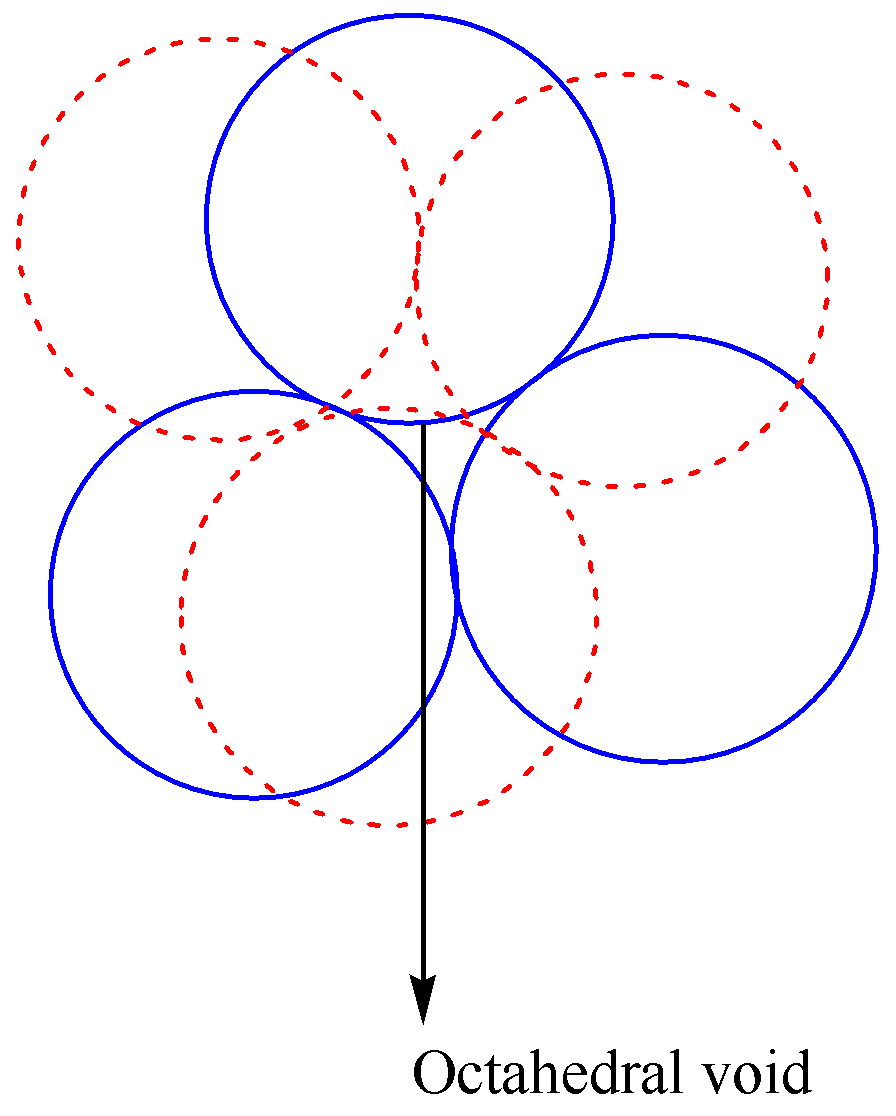
Note:
-We must remember that the voids in solid states mean the vacant between the atoms in a closely packed structure.
-Even in the closest packing of a sphere, there is some space left in between the spheres called interstitial sites.
Complete answer:
We can classify the close packing arrangements into square packing and hexagonal packing.
In the hexagonal arrangement, occupied space is
In square packing, arrangement of occupied space is
We have to remember that the arrangement of a solid sphere with close packing which remains some space is called voids.
-In three dimensions it shows interstitial sites in close packing of the sphere. Consider a triangular or trigonal site. Also of the above sites shows two different sites.
Now we discuss about the tetrahedral voids as,
-Tetrahedral sites: if three spheres are placed on the one spheres which are touching each other. Even four spheres touch one another some gaps available that know as the tetrahedral sites. In these sites, one sphere is surrounded by eight tetrahedral sites, and one site surrounded by four spheres. The coordination number is four and the ratio is
The diagram representation of tetrahedral voids is given as,

Now we discuss about the octahedral voids as,
Octahedral sites: The close packing of a sphere in hcp, as well as ccp arrangement, is known as octahedral sites. This shows six spheres attached in two forms. In these sites, one sphere is surrounded by six octahedral sites, and one site surrounded by six spheres. Hence the coordination number is six. Ratio is
The diagram representation of octahedral voids is given as,

Note:
-We must remember that the voids in solid states mean the vacant between the atoms in a closely packed structure.
-Even in the closest packing of a sphere, there is some space left in between the spheres called interstitial sites.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 12 Economics: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write a short note on Franklands reaction class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE




