Question

Why is mechanical advantage less than the velocity ratio of a real machine.

Answer 1

Hint: First go through the definition of mechanical advantage and velocity ratio and determine how it affects the working of a real machine. Understand the major difference between the two and find out the reason why mechanical advantage is always less than the velocity ratio.

Complete step by step answer:
In the question, we have two terms mainly mechanical advantage and velocity ratio, let us look at what these terms mean,

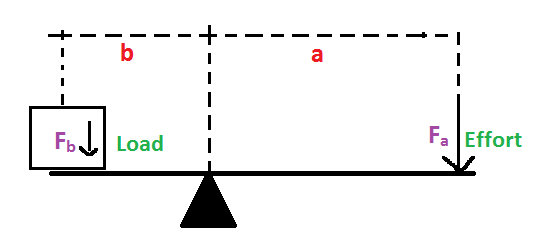
Mechanical Advantage: Mechanical advantage is the force amplification achieved by using a mechanical tool or mechanical system. This idea is derived from the law of the lever, given by Archimedes which states that,

“If the distance a from the fulcrum to where the input force is applied (point A) is greater than the distance b from the fulcrum to where the output force is applied (point B), then the lever amplifies the input force. If the distance from the fulcrum to the input force is less than from the fulcrum to the output force, then the lever reduces the input force.”

Suppose a and b are distances from the fulcrum to points and B respectively. ${{\text{F}}_{\text{A}}}$is the force acting on point A which is called the input force and ${{\text{F}}_{\text{B}}}$ is the force acting on point B which is called the output force, the mechanical advantage is the ratio of output force to the input force.

$\text{Mechanical Advantage (M}\text{.A)}=\dfrac{{{\text{F}}_{\text{B}}}}{{{\text{F}}_{\text{A}}}}=\dfrac{\text{a}}{\text{b}}$

The velocity ratio is the ratio of how fast the input force moves to how fast does the output force move. It can be written as,

$\text{Velocity Ratio}=\dfrac{{{\text{v}}_{\text{A}}}}{{{\text{v}}_{\text{B}}}}=\dfrac{\text{a}}{\text{b}}$

The velocity ratio is always a constant for a mechanical system, but the mechanical advantage varies because due to dissipative forces there can wear and tear in the system which causes a decrease in the output force as the machine keeps on working. So the mechanical advantage is always less than the velocity ratio for a real mechanical system.

Note: An ideal mechanism transmits power without adding to or subtracting from it. This means the ideal mechanism does not include a power source, is frictionless, and is constructed from rigid bodies that do not tear or wear. In this case, the mechanical advantage is equal to the velocity ratio.