Question

What is the minimum distance between an object and its real image in a convex lens (f = focal length of the lens)
(A). 2.5 f
(B). 2 f
(C). 4 f
(D). F

Answer 1

Hint- In order to deal with this question first we will use the concept that for real image the image and the object are on the opposite side of the lens so we will have to take v as positive and then we will proceed further by using thin lens formula.
Formula used- $\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f},D = {\left( b \right)^2} - 4a \times c{\text{ for general quadratic equation}}$.

Complete step-by-step solution -
Figure:

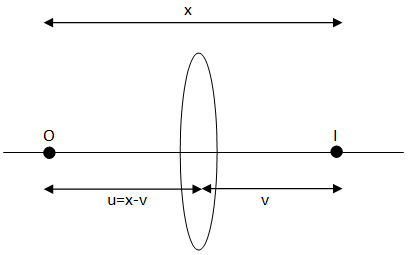
Look at the figure. Here, O is a point-like object and I is it’s image.
$u = $ Object distance.
$v = $ Image distance.
$f = $ Focal length of the lens.
$x = $ Distance between object and image.
We have to find the minimum value of x for which we can get the real image.
We know that for real image we will have to take v as positive and the lens formula is:
$\dfrac{1}{v} - \dfrac{1}{u} = \dfrac{1}{f}$----- (1)
Now, from the figure, $u = x - v$ . We substitute this value of u in equation (1), with remembering that according to Cartesian system of sign convention u is negative, we get
$
   \Rightarrow \dfrac{1}{v} - \dfrac{1}{{ - u}} = \dfrac{1}{f} \\
   \Rightarrow \dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f} \\
   \Rightarrow \dfrac{1}{v} + \dfrac{1}{{x - v}} = \dfrac{1}{f} \\
   \Rightarrow \dfrac{{x - v + v}}{{v\left( {x - v} \right)}} = \dfrac{1}{f} \\
   \Rightarrow \dfrac{x}{{v\left( {x - v} \right)}} = \dfrac{1}{f} \\
 $
Now let us cross multiply the equation to find the value of x
$
   \Rightarrow fx = vx - {v^2} \\
   \Rightarrow {v^2} - vx + fx = 0 \\
 $
We have to consider the condition for the real root of this quadratic equation in v.
From the above algebraic equation, we know that the roots will be real when the determinant of the quadratic equation will be greater than or equal to zero.
$
   \Rightarrow D \geqslant 0 \\
   \Rightarrow {\left( { - x} \right)^2} - 4xf \times 1 \geqslant 0{\text{ }}\left[ {\because D = {{\left( b \right)}^2} - 4a \times c{\text{ for general quadratic equation}}} \right] \\
   \Rightarrow {x^2} - 4xf \geqslant 0 \\
   \Rightarrow {x^2} \geqslant 4xf \\
   \Rightarrow x \geqslant 4f \\
 $
Thus, for real image by converging lens the minimum distance between object and image should be 4f, where f is focal length of the lens
Hence the correct answer is option C.

Note- Converging lens is a convex lens in which light rays that enter it parallel to its axis converge at a single point on the opposite side. Diverging lens is a concave lens in which light rays that enter the lens parallel to its axis bend away (diverge) from its axis. Lens formula is common for the entire lens and must be remembered by students to solve such problems. Also students must note that for the distance in the optics we commonly use the Cartesian system for sign convention.