Question

Moment of inertia of a uniform circular disc about a diameter is $I$. Its moment of inertia about an axis perpendicular to its plane and passing through a point on its rim will be:

Answer 1

Hint: The moment of inertia of a body is always specified with respect to a particular axis. The relation between the values of moment of inertia about different axIs can be determined using the two important axis theorems, the parallel axis theorem and the perpendicular axis theorem.

Complete answer:
While calculating the angular momentum of a rigid body, we need two important axis theorems:

(I)Parallel Axis Theorem:
For any plane rigid body, the moment of inertia about any of its axes which is perpendicular to the plane is equal to the sum of the moment of inertia about any two perpendicular axes in the plane of the body which intersect the first axis in the plane.

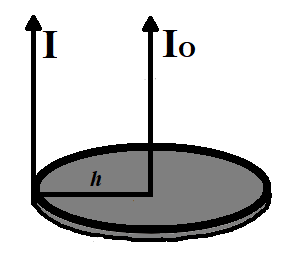
Expression for Parallel Axis theorem:
$I={{I}_{O}}+M{{h}^{2}}$
Where,
$I$ is the moment of inertia of the body
${{I}_{O}}$ is the moment of inertia about the center
$M$ is the mass of the body
$h$ is the distance between the two axes

(II)Perpendicular Axis Theorem:

Perpendicular axis theorem is used when the body is symmetric in shape about two out of the three axes. If the moment of inertia about two of the perpendicular axes is known, then the moment of inertia about the third axis is the sum of moment of inertia of the two perpendicular axes.

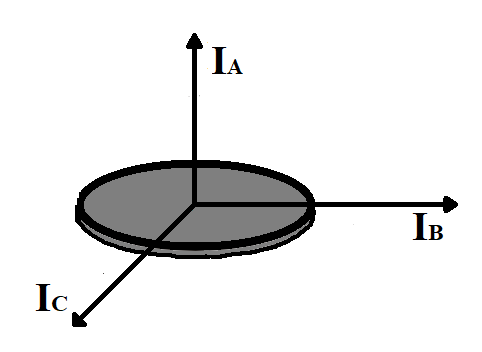
Expression for Perpendicular Axis theorem:
${{I}_{A}}={{I}_{B}}+{{I}_{C}}$
Where,
${{I}_{A}}$ is the moment of inertia along the axis in another plane
${{I}_{B}}$ and ${{I}_{C}}$are the moment of inertia along the two perpendicular axes
We are given the moment of inertia of a uniform circular disc about its diameter as $I$and we have to calculate its moment of inertia about an axis perpendicular to its plane and passing through a point on its rim.

Let $M$ and $R$ be the mass and radius of the disc respectively.

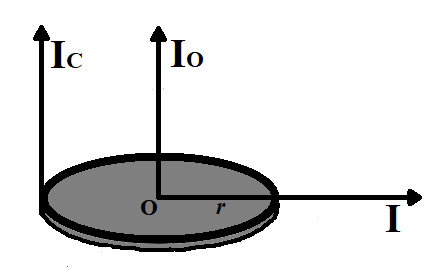
Moment of inertia about the axis AB is $I$
Using perpendicular axis theorem,
Moment of inertia about an axis passing through O and perpendicular to the plane is given as,
${{I}_{O}}=\dfrac{1}{2}M{{R}^{2}}$
Using parallel axis theorem,
Moment of inertia about an axis passing through C and perpendicular to the plane is given as,
${{I}_{C}}={{I}_{O}}+M{{R}^{2}}$
We have,
${{I}_{O}}=\dfrac{1}{2}M{{R}^{2}}$
Therefore,
$\begin{align}
  & {{I}_{C}}={{I}_{O}}+2{{I}_{O}} \\
 & {{I}_{C}}=3{{I}_{O}} \\
\end{align}$
Using perpendicular axis theorem,
${{I}_{O}}=2I$
Therefore,
${{I}_{C}}=6I$

The moment of inertia of a uniform circular disc about an axis perpendicular to its plane and passing through a point on its rim is six times the moment of inertia about its diameter.

Additional Information:
Moment of inertia is described as a quantitative measure of the rotational inertia of a body, that is, the opposition that the body exhibits against its speed of rotation about an axis altered by the application of a torque, or turning force. The axis of rotation may be internal or external and may or may not be fixed. The moment of inertia is always specified with respect to a particular axis and is defined as the sum of the products obtained by multiplying the mass of each particle of matter in a given object or body by the square of its distance from the axis.

In calculating the angular momentum for a rigid body, the moment of inertia of a body about an axis parallel to the body and passing through its center is equal to the sum of moment of inertia of body about the axis passing through the center and product of mass of the body times the square of distance between the two axes.

Note:
The moment of inertia in rotational dynamics is analogous to mass in linear dynamics. While calculating the moment of inertia of a rigid body, axis should be chosen carefully. The value of moment of inertia of a body varies upon altering the axis about which the value is being calculated.