
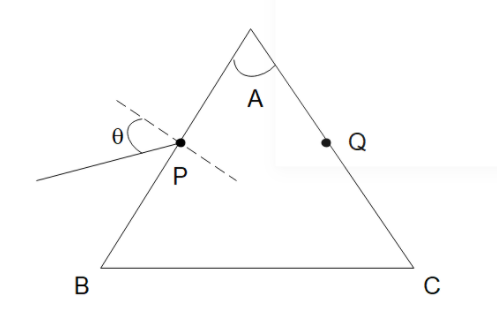
Monochromatic light is incident on a glass prism of angle A. If the refractive index of the material of the prism is \[\mu \], a ray incident at an angle \[\theta \], on the face AB would get transmitted through the face AC of the prism provided
A) \[\theta > si{n^{ - 1}}\left( {\mu sin\left( {A - si{n^{ - 1}}\left( {\dfrac{1}{\mu }} \right)} \right)} \right)\]
B) \[\theta < si{n^{ - 1}}\left( {\mu sin\left( {A - si{n^{ - 1}}\left( {\dfrac{1}{\mu }} \right)} \right)} \right)\]
C) \[\theta > {\cos ^{ - 1}}\left( {\mu sin\left( {A - si{n^{ - 1}}\left( {\dfrac{1}{\mu }} \right)} \right)} \right)\]
D) \[\theta < {\cos ^{ - 1}}\left( {\mu sin\left( {A - si{n^{ - 1}}\left( {\dfrac{1}{\mu }} \right)} \right)} \right)\]
Answer
232.8k+ views
Hint: In this solution, we will use Schell’s law of refraction to determine the angle of refraction when the ray of light passes from the surface AB. This angle of refraction from the first surface should be such that the angle of incidence on the surface AC will be such that the ray will be internally reflected.
Formula used: In this solution, we will use the following formula:
Snell's law: ${\mu _1}\sin {\theta _1} = {\mu _2}\sin {\theta _2}$ where ${\mu _1}$ and ${\mu _2}$ are the refractive index of two different mediums and ${\theta _1}$ and ${\theta _2}$ are the angles made by the ray of light with the normal to the surface of refraction.
Complete step by step answer:
Let the angle of incidence on the surface AB be $\theta $. Then using Snell’s law on the first surface, the incident medium will be air so its refractive index will be 1.
$1\sin \theta = \mu \sin r$
Now the angle of incidence on the other surface will be $r'$. The relation between $r$ and $r'$ will be determined from the triangle APQ as the sum of all the angles in the triangle will be $180^\circ $.
$A + (90^\circ - r) + (90^\circ - r') = 180$
Which gives us
$r' = A - r$
Now for the surface, AC, the angle of incidence on the surface $r'$ will be such that the angle of reflection will be $90^\circ $ or greater which implies
$\mu \sin r' < 1\sin 90^\circ $
So, dividing both sides by $\mu $ and taking the sine inverse on both sides, we get
$r' < {\sin ^{ - 1}}\dfrac{1}{\mu }$
Since $r' = A - r$, we can write
$A - r < {\sin ^{ - 1}}\dfrac{1}{\mu }$
$r > A - {\sin ^{ - 1}}\dfrac{1}{\mu }$
Again as $1\sin \theta = \mu \sin r$, we can write
\[\theta > si{n^{ - 1}}\left( {\mu sin\left( {A - si{n^{ - 1}}\left( {\dfrac{1}{\mu }} \right)} \right)} \right)\] which corresponds to option (A).
Note: To solve such questions, we must be aware of the phenomenon of internal reflection and how it behaves in a prism. Unless mentioned otherwise, we must assume the medium outside the prism to be air and have a refractive index of 1.
Formula used: In this solution, we will use the following formula:
Snell's law: ${\mu _1}\sin {\theta _1} = {\mu _2}\sin {\theta _2}$ where ${\mu _1}$ and ${\mu _2}$ are the refractive index of two different mediums and ${\theta _1}$ and ${\theta _2}$ are the angles made by the ray of light with the normal to the surface of refraction.
Complete step by step answer:
Let the angle of incidence on the surface AB be $\theta $. Then using Snell’s law on the first surface, the incident medium will be air so its refractive index will be 1.
$1\sin \theta = \mu \sin r$
Now the angle of incidence on the other surface will be $r'$. The relation between $r$ and $r'$ will be determined from the triangle APQ as the sum of all the angles in the triangle will be $180^\circ $.
$A + (90^\circ - r) + (90^\circ - r') = 180$
Which gives us
$r' = A - r$
Now for the surface, AC, the angle of incidence on the surface $r'$ will be such that the angle of reflection will be $90^\circ $ or greater which implies
$\mu \sin r' < 1\sin 90^\circ $
So, dividing both sides by $\mu $ and taking the sine inverse on both sides, we get
$r' < {\sin ^{ - 1}}\dfrac{1}{\mu }$
Since $r' = A - r$, we can write
$A - r < {\sin ^{ - 1}}\dfrac{1}{\mu }$
$r > A - {\sin ^{ - 1}}\dfrac{1}{\mu }$
Again as $1\sin \theta = \mu \sin r$, we can write
\[\theta > si{n^{ - 1}}\left( {\mu sin\left( {A - si{n^{ - 1}}\left( {\dfrac{1}{\mu }} \right)} \right)} \right)\] which corresponds to option (A).
Note: To solve such questions, we must be aware of the phenomenon of internal reflection and how it behaves in a prism. Unless mentioned otherwise, we must assume the medium outside the prism to be air and have a refractive index of 1.
Recently Updated Pages
JEE Main 2023 April 6 Shift 1 Question Paper with Answer Key

JEE Main 2023 April 6 Shift 2 Question Paper with Answer Key

JEE Main 2023 (January 31 Evening Shift) Question Paper with Solutions [PDF]

JEE Main 2023 January 30 Shift 2 Question Paper with Answer Key

JEE Main 2023 January 25 Shift 1 Question Paper with Answer Key

JEE Main 2023 January 24 Shift 2 Question Paper with Answer Key

Trending doubts
JEE Main 2026: Session 2 Registration Open, City Intimation Slip, Exam Dates, Syllabus & Eligibility

JEE Main 2026 Application Login: Direct Link, Registration, Form Fill, and Steps

JEE Main Marking Scheme 2026- Paper-Wise Marks Distribution and Negative Marking Details

Understanding the Angle of Deviation in a Prism

Hybridisation in Chemistry – Concept, Types & Applications

How to Convert a Galvanometer into an Ammeter or Voltmeter

Other Pages
JEE Advanced Marks vs Ranks 2025: Understanding Category-wise Qualifying Marks and Previous Year Cut-offs

Laws of Motion Class 11 Physics Chapter 4 CBSE Notes - 2025-26

Waves Class 11 Physics Chapter 14 CBSE Notes - 2025-26

Mechanical Properties of Fluids Class 11 Physics Chapter 9 CBSE Notes - 2025-26

Thermodynamics Class 11 Physics Chapter 11 CBSE Notes - 2025-26

Units And Measurements Class 11 Physics Chapter 1 CBSE Notes - 2025-26




