Question

Mr. Hassan’s gate has a diagonal bracing strut to strengthen it. What is the length of this bracing strut?

Answer 1

Hint: In the given figure, we are asked to find the length of the diagonal bracing strut. As you can see that the diagonal bracing strut and the two perpendicular supports are forming a right-angled triangle in which the diagonal bracing strut is acting as a hypotenuse. We are going to use the Pythagoras theorem to find the length of the diagonal bracing strut. In Pythagoras theorem, the square of the hypotenuse is equal to the sum of the square of the base and the square of the perpendicular.

Complete step by step answer:
The figure, given in the above problem is as follows:

Now, we are going to name the corners of the above figure and it will look like this:

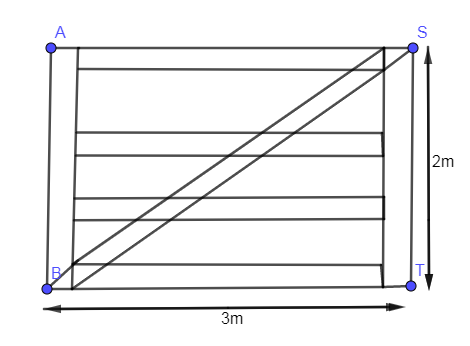
In the above problem, we are asked to find the length of the diagonal bracing strut which we have shown by (SB). As you can see that the diagonal bracing strut (BS) along with the two perpendicular supports (BT and ST) are forming a right angles triangle which is right angled at T. So, we are going to use the Pythagoras theorem to find the length of the diagonal BS.
We know that according to Pythagoras theorem, the square of the hypotenuse is equal to the sum of the square of base and square of perpendicular.
${{\left( Hypotenuse \right)}^{2}}={{\left( Base \right)}^{2}}+{{\left( Perpendicular \right)}^{2}}$
Now, substituting hypotenuse as BS, base as (BT) and perpendicular as (ST) in the above equation and we get,
${{\left( BS \right)}^{2}}={{\left( BT \right)}^{2}}+{{\left( ST \right)}^{2}}$
Substituting BT as 3m and ST as 2m in the above equation we get,
$\begin{align}
  & {{\left( BS \right)}^{2}}={{\left( 3 \right)}^{2}}+{{\left( 2 \right)}^{2}} \\
 & \Rightarrow {{\left( BS \right)}^{2}}=9+4 \\
 & \Rightarrow {{\left( BS \right)}^{2}}=13......(1) \\
\end{align}$
Taking square root on both the sides of the above equation we get,
$BS=\sqrt{13}m$
From the above, we have solved the value of the bracing strut as $\sqrt{13}m$.

Note: To solve the above problem, you must know the Pythagoras theorem otherwise you cannot solve this problem. So, make sure you have properly understood the concept of Pythagoras theorem. Also, a mistake that could be a possibility while solving this problem is that you might forget to take the square root in the last step so make sure you have taken the square root in the final answer.