Question

What must be the angular velocity of rotation of the earth so that the effective acceleration due to gravity at the equator is zero? The radius of the earth = $64 \times {10^4}\,m$ .
A. $3.3 \times {10^{ - 3}}\,rad\,{s^{ - 1}}$
B. $3.5 \times {10^{ - 3}}\,rad\,{s^{ - 1}}$
C. $3.7 \times {10^{ - 3}}\,rad\,{s^{ - 1}}$
D. $3.9 \times {10^{ - 3}}\,rad\,{s^{ - 1}}$

Answer 1

Hint: For any particle in the gravitational field of another particle, the gravitational force experienced by that particle is based on the distance from the axis of that large particle. Any substance in a gravitational field experiences a bunch of forces namely, gravitational, centripetal, and centrifugal. The resultant of all the forces gives intensity of gravitational force on that substance.

Complete step by step solution:
To know the angular velocity with which earth should rotate, we must first have to evaluate the relation between angular velocity and gravitational force based on degree of latitude. Imagine this as earth surrounding and pulling a small particle at degree a above equator,

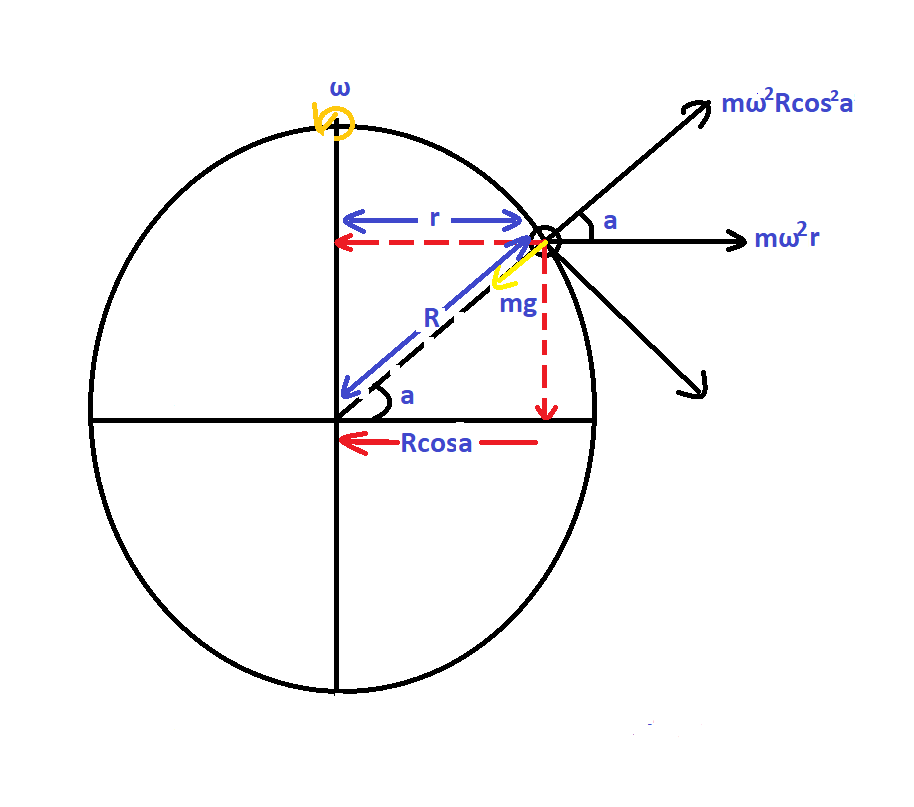
Force on particle due to rotational motion is given as,
$m{\omega ^2}r$
Where, $m = \,{\text{mass}}\,{\text{of}}\,{\text{particle}}$
$\omega = \,{\text{angular}}\,{\text{velocity}}\,{\text{at}}\,{\text{which}}\,{\text{the}}\,{\text{particle}}\,{\text{rotate}}$
$r = \,{\text{distance}}\,{\text{of}}\,{\text{particle}}\,{\text{from}}\,{\text{axis}}\,{\text{of}}\,{\text{rotation}}$
Here it is important to notice that distance of angular force isn’t taken as earth centre but the axis about which it rotates (rotational motion).
Now substitute the angular force into two parts one being parallel and opposite to gravitational pull balancing it to keep the particle firm in its radius. Another substitution will balance centrifugal force on particles preventing particles from leaving its site to vanish in space.
Centrifugal force is not necessary in this part hence only part of force parallel and opposite to centripetal force is included in the equations.
${\text{Evaluation}}\,{\text{of}}\,{\text{rotational}}\,{\text{force}} = m{\omega ^2}r\cos a$ \[\]
From the figure it is evident that $r = R\cos a$
Placing value of r in equation, we get
${\text{Evaluation}}\,{\text{of}}\,{\text{rotational}}\,{\text{force}} = m{\omega ^2}R{\cos ^2}a$ \[\]
Now the diagram clearly shows that the particle is situated at a particular latitude and as we change our position slightly from any degree on earth - the value of intensity of gravitational field also varies. It implies that the weight of the substance on a specific latitude is not $mg$ but it is variant based on amount of latitude substance has covered, hence our rotational force can be now evaluated as,
 Where,
$g = \,{\text{gravitational}}\,{\text{force}}\,{\text{intensity}}\,{\text{of}}\,{\text{earth}}$
The above equation (i) gives us the relation between angular velocity and gravitational pull and is a very important concept and equation to be understood.
Now as per our question we need to find the angular speed at which gravitational force intensity become zero i.e.
Putting value of in equation (i)
$0 = g - {\omega ^2}R{\cos ^2}a$
Taking ${\omega ^2}R{\cos ^2}a$ to left hand side,
${\omega ^2}R{\cos ^2}a = g$
As the particle is to be at equator hence,
Putting value of $g = 10\,m\,{s^{ - 2}}$ , $R = 64 \times {10^4}m$ , $a = {0^o}$
${\omega ^2} \times 64 \times {10^4} \times {\cos ^2}0 = 10$
Evaluating equation gives,
${\omega ^2} = \dfrac{1}{{64000}}$
$\omega = 3.9 \times {10^{ - 3}}\,rad\,{s^{ - 1}}$
Correct answer is option (D) $\omega = 3.9 \times {10^{ - 3}}\,rad\,{s^{ - 1}}$.

Note:
Before attempting the question it is very important to know the relation between gravitational force and angular velocity. Besides this the variation in gravitational force with latitude is a very important factor on which this whole equation and question depends. Managing gravitational and rotational is a bit typical but clearance in basics makes it easy to focus on the matter.