
Answer
421.8k+ views
Hint: This question involves the arithmetic operations like addition/ subtraction/ multiplication/ division. We need to know how to draw a graph for the given equation. Also, we need to know how to find \[x\& y\] from the given equation to make an easy calculation for the given question. Also, we need to know how to plot the points in the graph.
Complete step-by-step answer:
To find the nature of the graph we would draw the graph for the given equation.
For that, we would assume \[x = ...., - 2, - 1,0,1,2,...\]
We have \[y = \dfrac{4}{x} \to \left( 1 \right)\]
Let’s take \[x = - 2\] in the equation \[\left( 1 \right)\] , we get
\[\left( 1 \right) \to y = \dfrac{4}{x}\]
\[
y = \dfrac{4}{{ - 2}} \\
y = - 2 \;
\]
Let’s take \[x = - 1\] in the equation \[\left( 1 \right)\] , we get
\[\left( 1 \right) \to y = \dfrac{4}{x}\]
\[
y = \dfrac{4}{{ - 1}} \\
y = - 4 \;
\]
Let’s take \[x = 0\] in the equation \[\left( 1 \right)\] , we get
\[\left( 1 \right) \to y = \dfrac{4}{x}\]
\[
y = \dfrac{4}{0} \\
y = \infty \;
\]
Let’s take \[x = 1\] in the equation \[\left( 1 \right)\] , we get
\[\left( 1 \right) \to y = \dfrac{4}{x}\]
\[
y = \dfrac{4}{1} \\
y = 4 \;
\]
Let’s take \[x = 2\] in the equation \[\left( 1 \right)\] , we get
\[\left( 1 \right) \to y = \dfrac{4}{x}\]
\[
y = \dfrac{4}{2} \\
y = 2 \;
\]
Let’s make a tabular column with various \[x\& y\] values as given below,
By using the above tabular column we can make the following graph,
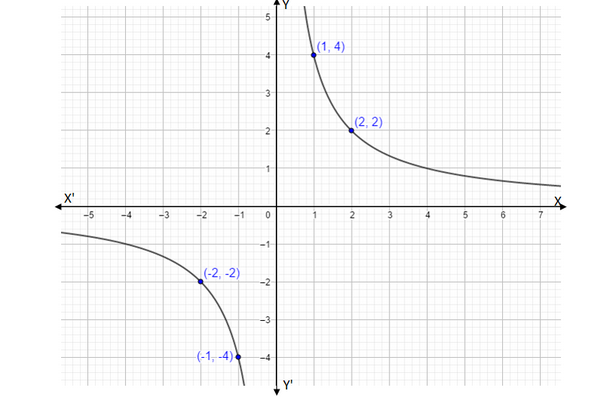
The above graph defines the equation \[y = \dfrac{4}{x}\] . In the above graph, we can see that the rectangular hyperbola is present in the first quadrant and third quadrant.
So, the final answer is,
\[A)\] Rectangular hyperbola in first and third quadrant
So, the correct answer is “OPTION A ”.
Note: This question describes the arithmetic operations like addition/ subtraction/ multiplication/ division. Note that to solve these types of questions we would draw the graph for the given equation. Also, note that for finding the value \[y\] we have to assume the \[x\] values. By using \[x\& y\] values we can easily draw the graph.
Complete step-by-step answer:
To find the nature of the graph we would draw the graph for the given equation.
For that, we would assume \[x = ...., - 2, - 1,0,1,2,...\]
We have \[y = \dfrac{4}{x} \to \left( 1 \right)\]
Let’s take \[x = - 2\] in the equation \[\left( 1 \right)\] , we get
\[\left( 1 \right) \to y = \dfrac{4}{x}\]
\[
y = \dfrac{4}{{ - 2}} \\
y = - 2 \;
\]
Let’s take \[x = - 1\] in the equation \[\left( 1 \right)\] , we get
\[\left( 1 \right) \to y = \dfrac{4}{x}\]
\[
y = \dfrac{4}{{ - 1}} \\
y = - 4 \;
\]
Let’s take \[x = 0\] in the equation \[\left( 1 \right)\] , we get
\[\left( 1 \right) \to y = \dfrac{4}{x}\]
\[
y = \dfrac{4}{0} \\
y = \infty \;
\]
Let’s take \[x = 1\] in the equation \[\left( 1 \right)\] , we get
\[\left( 1 \right) \to y = \dfrac{4}{x}\]
\[
y = \dfrac{4}{1} \\
y = 4 \;
\]
Let’s take \[x = 2\] in the equation \[\left( 1 \right)\] , we get
\[\left( 1 \right) \to y = \dfrac{4}{x}\]
\[
y = \dfrac{4}{2} \\
y = 2 \;
\]
Let’s make a tabular column with various \[x\& y\] values as given below,
| \[x\] | \[ - 2\] | \[ - 1\] | \[0\] | \[1\] | \[2\] |
| \[y\] | \[ - 2\] | \[ - 4\] | \[\infty \] | \[4\] | \[2\] |
By using the above tabular column we can make the following graph,

The above graph defines the equation \[y = \dfrac{4}{x}\] . In the above graph, we can see that the rectangular hyperbola is present in the first quadrant and third quadrant.
So, the final answer is,
\[A)\] Rectangular hyperbola in first and third quadrant
So, the correct answer is “OPTION A ”.
Note: This question describes the arithmetic operations like addition/ subtraction/ multiplication/ division. Note that to solve these types of questions we would draw the graph for the given equation. Also, note that for finding the value \[y\] we have to assume the \[x\] values. By using \[x\& y\] values we can easily draw the graph.
Recently Updated Pages
How is abiogenesis theory disproved experimentally class 12 biology CBSE

What is Biological Magnification

Explain the Basics of Computer and Number System?

Class 11 Question and Answer - Your Ultimate Solutions Guide

Write the IUPAC name of the given compound class 11 chemistry CBSE

Write the IUPAC name of the given compound class 11 chemistry CBSE

Trending doubts
Who was the Governor general of India at the time of class 11 social science CBSE

Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

State and prove Bernoullis theorem class 11 physics CBSE

Proton was discovered by A Thomson B Rutherford C Chadwick class 11 chemistry CBSE

What organs are located on the left side of your body class 11 biology CBSE

10 examples of friction in our daily life




