Question

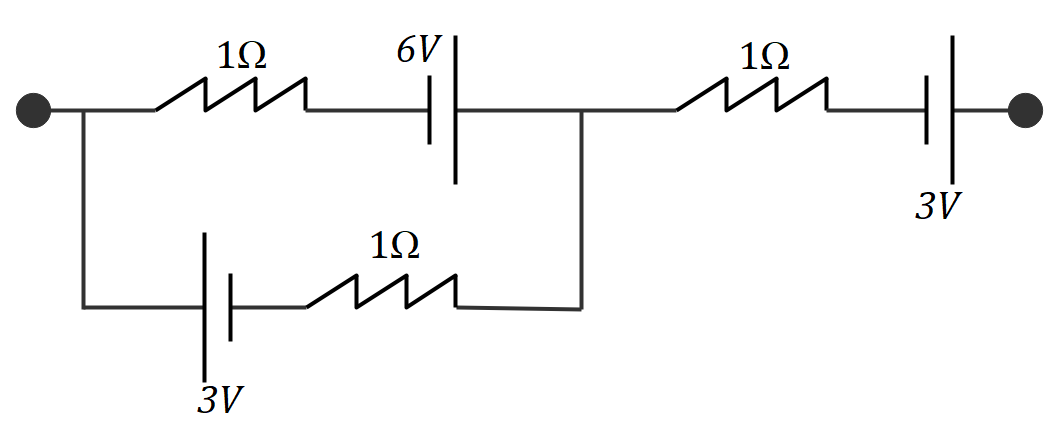
Net EMF and internal resistance of following circuit is:-

A. $\dfrac{7}{2}V,\dfrac{1}{2}\Omega $
B. $\dfrac{7}{2}V,\dfrac{3}{2}\Omega $
C. $\dfrac{9}{2}V,\dfrac{3}{2}\Omega $
D. $\dfrac{9}{2}V,\dfrac{1}{2}\Omega $

Answer 1

Hint: In the question, they’ve given us a connection of batteries with internal resistances. To find the total voltage across the battery, we have to know the total current drawn by the circuit and the total internal resistance offered by the circuit. We can apply KVL for the given circuit twice, each time considering a different branch of the circuit. And, find the total resistance. From, ohm’s law we’ll have the net emf of the circuit.

Complete answer:
Let us redraw the given circuit with proper labeling.

From the diagram, given in the question let us that the endpoints are A and B. Then, the net emf across the circuit will be VAB. If a current I is the total current flowing through the circuit. And, say, current I1 enters the branch PQ. Then, the current through the branch RS will be I-I1.
Now, let us apply Kirchhoff’s voltage law across the path APQB. Then we’ll have,
${V_A} + {I_1} \times 1\Omega - 6V + {I_1} \times 1\Omega - 3V - {V_B} = 0 - - > eq.1$
Similarly, if we apply Kirchhoff’s voltage law across the path ARSB, we’ll have
${V_A} + 3V + \left( {I - {I_1}} \right) \times 1\Omega + {I_1} \times 1\Omega - 3V - {V_B} = 0 - - > eq.2$
Solving these both equations, we’ll have the current across the ends AB as, $I = 3A$.
From the circuit diagram, one can understand that the resistances across AB and RS are connected in parallel to each other and the resistance between the ends QB is in series with both. Hence, the total internal resistance of the circuit will be
$\eqalign{
  & {r_{AB}} = \dfrac{{{r_{PQ}}{r_{RS}}}}{{{r_{PQ}} + {r_{RS}}}} + {r_{QB}} \cr
  & \Rightarrow {r_{AB}} = \dfrac{{1 \times 1}}{{1 + 1}} + 1 \cr
  & \Rightarrow {r_{AB}} = \dfrac{1}{2} + 1 \cr
  & \Rightarrow {r_{AB}} = \dfrac{3}{2}\Omega \cr} $
From this, we’ll have the net emf of the circuit using ohm’s law as
$\eqalign{
  & {V_{AB}} = I \times {r_{AB}} \cr
  & \Rightarrow {V_{AB}} = 3A \times \dfrac{3}{2}\Omega \cr
  & \Rightarrow {V_{AB}} = \dfrac{9}{2}V \cr} $
Therefore, the net emf of the circuit is $\dfrac{9}{2}V$ and the net internal resistance is $\dfrac{3}{2}\Omega $.

So, the correct answer is “Option C”.

Note:
Kirchhoff’s voltage law states that the algebraic sum of voltages across a closed loop is zero. Even though there’s no closed loop in the circuit, we can imagine a primary cell connected to the ends AB, to avoid confusion. One should also pay attention to the battery’s terminal while applying Kirchhoff’s Voltage Law.