Question

How many nodes are present in 3-p orbitals? Represent diagrammatically.

Answer 1

Hint: We have to know there are two kinds of nodes, angular and radial nodes. Angular nodes are flat planes (at fixed angles). The “l” angular quantum number gives the number of angular nodes in an orbital. We can say radial nodes are spheres (at fixed radius), which is seen with an increase in the principal quantum number. The sum of angular and radial nodes gives the total number of nodes of an orbital.
Formula used: We calculate the total number of nodes in an orbital using the equation:
$N = n - 1$
Here, N=Total number of nodes
n=principal quantum number

Complete step by step answer:
We have to know that 3p orbital the principal quantum number $n = 3$, placing it on the third energy level and the angular quantum number \[l = 1\] gives the shape of p-orbital.
We can calculate the number of radial nodes using the formula,
$N = n - l - 1$
The value of n is 3 and the value of l is 1.
$N = 3 - 1 - 1$
$N = 1$
The number of radial nodes in 3p orbitals is one.
We have to know that the number of angular nodes could be determined by the angular quantum number l.
The number of angular nodes is expressed by l. So \[l = 1\].
The number of angular nodes in 3p orbitals is one.
The total number of nodes present in 3p orbital is calculated using the equation,
$N = n - 1$
We know the value of n is 3.
So the total number of nodes present is calculated as,
$N = n - 1$
$N = 3 - 1$
$N = 2$
The total number of nodes present in a 3p orbital is two.
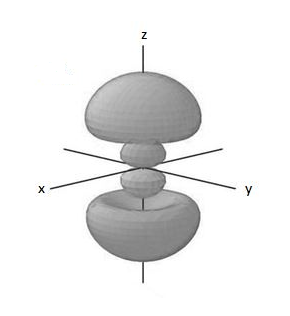
Therefore, in a 3p orbital there is one angular node and one radial node.
The diagrammatic representation is,

Note:
Let us now determine the number of angular and radial nodes of 4f orbital.
In a 4f orbital, the principal quantum number is 4 and the angular quantum number is 3 ($n = 4$,$l = 3$). Therefore, the number of angular nodes present in 3.
We can now calculate the total number of nodes in 4f orbital as,
$N = n - 1$
Here, the value of n will be 4.
$N = n - 1$
$N = 4 - 1$
$N = 3$
This means there will be no radial nodes present in 4f orbital.
We have to know that the value of the angular quantum number has a little effect on the energy of the subshell, the energy of the subshell increases with l (sWe can describe the electrons in an atom using four quantum numbers.
-Principal Quantum number (n)
-Angular (azimuthal) quantum number (l)
-Magnetic quantum number (m)
-Spin quantum number (s)