
Now use numbers 1-6 to make your own magic triangle.
Rule: Numbers on each side must add up to 10.

Answer
571.2k+ views
Hint: Magic triangle is a triangle with vacant places to fill with numbers on corners and on each side. The property of a magic triangle is that the sum of all numbers on each side must be the same. One of the methods we can try is the trial and error as the numbers to be used is smaller in count. Thus we will try to start with a particular corner and then fill one by one checking whether each side adds up to 10 or not.
Complete step-by-step answer:
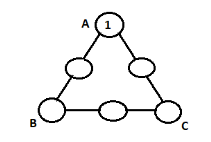
Step 1: Let us start by naming the triangle as triangle ABC. We have 6 vacant places which are to be filled with numbers 1-6 having 3 corners. Then the triangle with number 1 filled on corner A will be as below:
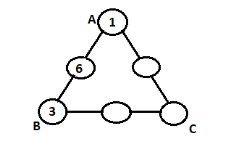
Step 2: As 6 and 4 together add up to 10, we cannot put them on the same side of the triangle. Thus if we choose 6 on side AB, 4 should be placed on side BC or AC. Filling 6 on middle position of side AB, clearly corner B will be filled by 10-(6+1)=3. Thus the triangle will look like,
Step 3: Now if we fill 4 on side BC, then 3+4 add up to 7 and the rest of the vacant place of side BC should be filled by 10-7 which is 3 which have already been used for corner B. Thus 4 can only be placed on the middle vacancy of side AC. Then corner C will be filled by 10-(4+1)=5. Thus the triangle will look like,
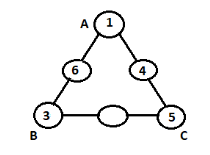
Step 4: Now the only remaining position is middle vacancy of side BC and the remaining number is 2. Let us check the sum of numbers of side BC if 2 is filled, which will be 3+2+5=10. Thus our aim is achieved. Thus the final form of triangle will be,
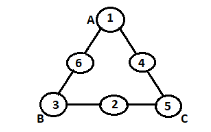
Final answer: The magic triangle using numbers 1-6 with sides adding upto 10 is :
Note: Solving time may increase if we try to fill the numbers randomly. Thus while placing each number, we must rule out the chance of placing other number on the same side.
As we have seen a magic triangle in the above solution, there are some other similar figures having the same property. One of which is Magic square which is a square split either by 9 vacant places inside of 16 according to the solution we require. Let us see one example of a 3*3 magic square:
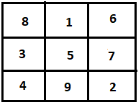
Above is a magic square with 9 vacant places filled with numbers 1-9 with each side and diagonal adding upto 15.
Complete step-by-step answer:
Step 1: Let us start by naming the triangle as triangle ABC. We have 6 vacant places which are to be filled with numbers 1-6 having 3 corners. Then the triangle with number 1 filled on corner A will be as below:

Step 2: As 6 and 4 together add up to 10, we cannot put them on the same side of the triangle. Thus if we choose 6 on side AB, 4 should be placed on side BC or AC. Filling 6 on middle position of side AB, clearly corner B will be filled by 10-(6+1)=3. Thus the triangle will look like,

Step 3: Now if we fill 4 on side BC, then 3+4 add up to 7 and the rest of the vacant place of side BC should be filled by 10-7 which is 3 which have already been used for corner B. Thus 4 can only be placed on the middle vacancy of side AC. Then corner C will be filled by 10-(4+1)=5. Thus the triangle will look like,

Step 4: Now the only remaining position is middle vacancy of side BC and the remaining number is 2. Let us check the sum of numbers of side BC if 2 is filled, which will be 3+2+5=10. Thus our aim is achieved. Thus the final form of triangle will be,

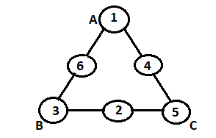
Final answer: The magic triangle using numbers 1-6 with sides adding upto 10 is :

Note: Solving time may increase if we try to fill the numbers randomly. Thus while placing each number, we must rule out the chance of placing other number on the same side.
As we have seen a magic triangle in the above solution, there are some other similar figures having the same property. One of which is Magic square which is a square split either by 9 vacant places inside of 16 according to the solution we require. Let us see one example of a 3*3 magic square:

Above is a magic square with 9 vacant places filled with numbers 1-9 with each side and diagonal adding upto 15.
Recently Updated Pages
You are awaiting your class 10th results Meanwhile class 7 english CBSE

Master Class 7 Social Science: Engaging Questions & Answers for Success

Master Class 7 Science: Engaging Questions & Answers for Success

Class 7 Question and Answer - Your Ultimate Solutions Guide

Master Class 7 English: Engaging Questions & Answers for Success

Master Class 7 Maths: Engaging Questions & Answers for Success

Trending doubts
Full Form of IASDMIPSIFSIRSPOLICE class 7 social science CBSE

Convert 200 Million dollars in rupees class 7 maths CBSE

i What trees does Mr Wonka mention Which tree does class 7 english CBSE

What are the controls affecting the climate of Ind class 7 social science CBSE

Write a letter to the editor of the national daily class 7 english CBSE

Welcome speech for Christmas day celebration class 7 english CBSE





