Question

Where should the object be placed in front of the concave mirror so that image is as the same size as the object
A. Focus
B. At infinity
C. At center of curvature
D. None of the above

Answer 1

Hint: Students must have knowledge of the mirror formula which relates the object position, to the image position and the focal length. Knowledge of the sign conventions is also important. Knowledge of mirror magnification. The radius of curvature of a spherical mirror is twice the focal length.

Formula used:
The mirror Formula: $\dfrac{1}{u} + \dfrac{1}{v} = \dfrac{1}{f}$
The magnification for a mirror is given as, $m = - \dfrac{v}{u}$

Complete answer:
Let us assume that the object is on the left side of the mirror. We want the image to be the same size as the object. Therefore, the magnitude of magnification must be 1.
And, using the magnification formula, $m = - \dfrac{v}{u}$,
For $m = - 1$, …(1),
We put the value of magnification as negative of 1 because the image formed by the mirror must be inverted when it is real.
Now, using the mirror formula,

$\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$
From equation (1)

$\eqalign{
  & \dfrac{1}{u} + \dfrac{1}{u} = \dfrac{1}{f} \cr
  & \Rightarrow \dfrac{2}{u} = \dfrac{1}{f} \cr
  & \Rightarrow u = 2f \cr} $
Now, we know that the radius of curvature is twice the distance of the focal length from the mirror.
Hence, the object must be placed at the center of curvature. The following ray diagram shows the set up for the same.

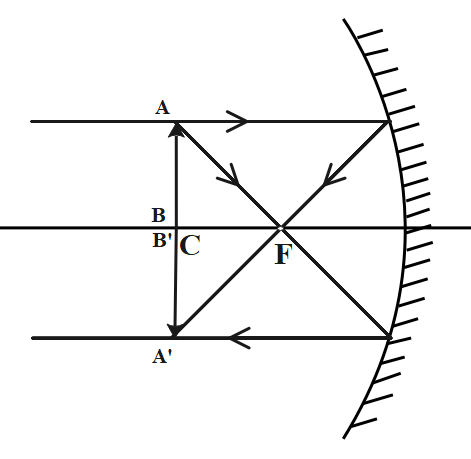
Therefore, the correct option C i.e. the object should be placed at the center of curvature of the concave mirror so that image is the same size as the object.

So, the correct answer is “Option C”.

Note:
Students can make mistakes by assuming the value of magnitude as 1 instead of minus 1. So, they must remember that, for the image to have the same size as the object, the image must be real and hence inverted, which means the magnification will be minus 1.