
When object is placed in between convex lens and its focal point, image formed is
A. Diminishes, real and inverted
B. Same size, real and inverted
C. Same size, real and upright
D. Magnified, virtual and upright
Answer
488.7k+ views
Hint: Position of image formed can be found using lens formula. We can use a magnification formula to determine the size ratio of the image to object.
A ray diagram can also be used to determine the details about the image.
Formula Used:
Lens formula,
Complete answer:
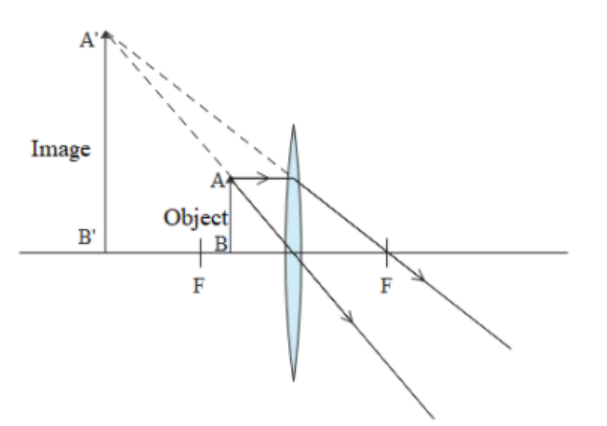
Above diagram is for the Formation of an image by a convex lens when the object is placed between focal point and optical centre.
The object is placed between the optical centre of the convex lens and its focal point. Therefore, the magnitude of distance of object from the optical centre,
Where
The focal length of the convex lens is positive and object distance is taken negative as per sign convention. The lens formula is given by
Where
Since
Since
From lens formula, we get
From this, we can conclude that the image is formed on the left side as image distance is negative.
Now magnification of image if h’ and h are heights of image and object respectively,
Since
Because
Hence, option D is correct.
Note:
In mirror as well as optical lens problems, the most important thing to consider is sign conventions. Therefore, students should understand the sign conventions properly and then proceed with the solution. Diagrams are very helpful in understanding the sign conventions.
Focal length of a convex lens is always taken positively.
A ray diagram can also be used to determine the details about the image.
Formula Used:
Lens formula,
Complete answer:

Above diagram is for the Formation of an image by a convex lens when the object is placed between focal point and optical centre.
The object is placed between the optical centre of the convex lens and its focal point. Therefore, the magnitude of distance of object from the optical centre,
Where
The focal length of the convex lens is positive and object distance is taken negative as per sign convention. The lens formula is given by
Where
Since
Since
From lens formula, we get
From this, we can conclude that the image is formed on the left side as image distance is negative.
Now magnification of image if h’ and h are heights of image and object respectively,
Since
Because
Hence, option D is correct.
Note:
In mirror as well as optical lens problems, the most important thing to consider is sign conventions. Therefore, students should understand the sign conventions properly and then proceed with the solution. Diagrams are very helpful in understanding the sign conventions.
Focal length of a convex lens is always taken positively.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE




