Question

How many obtuse angles does a parallelogram have?

Answer 1

Hint: Here in this question, we need to find the number of obtuse angles formed in a parallelogram. Obtuse Angles are the angles that are more than ${{90}^{\circ }}$. Parallelogram is basically a quadrilateral having four sides and four angles.

Complete step by step answer:
Now, let’s have a look at the question:

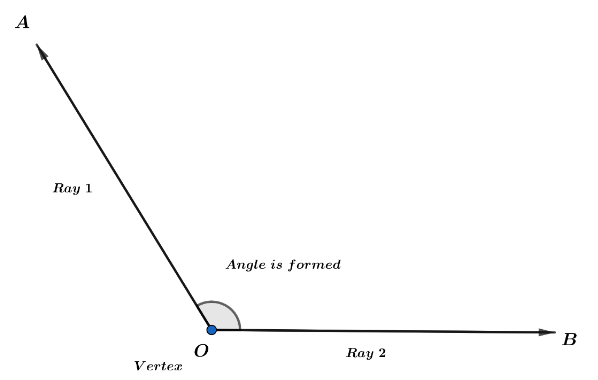
As we know that when the two rays meet at a vertex, an angle is formed and it is represented by the symbol $\angle $ and is measured in degrees.
We also know what an obtuse angle is!
The angle whose measure is greater than ${{90}^{\circ }}$ and lesser than ${{180}^{\circ }}$ is called an obtuse angle.
Let’s see some of the examples of obtuse angle:

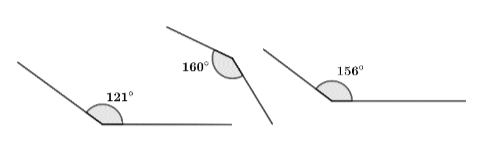
So, the angles ${{121}^{\circ }},{{160}^{\circ }},{{156}^{\circ }}$ can be called as Obtuse Angles.

Real-life example: In real life, when the minute hand of the clock is at 10 and the hour hand is at 3, then the angle formed between 10-3 clockwise will be an obtuse angle.
Now, let’s come to parallelogram:
The parallelogram is basically a simple quadrilateral having two pairs of parallel sides, opposite sides equal lengths and equal opposite angles.
You should know that the sum of the interior angles of any quadrilateral is ${{180}^{\circ }}$.
Thus, consecutive angles are supplementary and the opposite angles are equal.

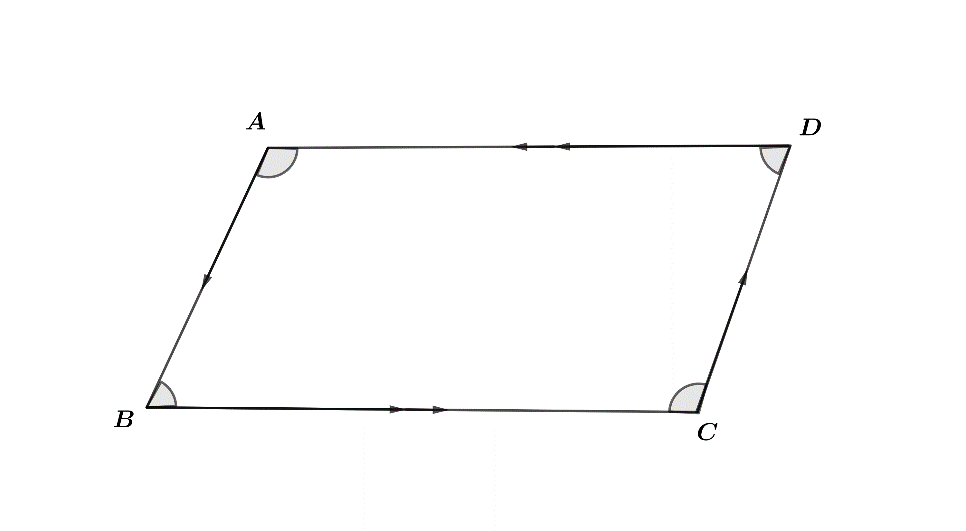
So, from the figure, we can see that there are only two obtuse angles (i.e. $\angle $ A & $\angle $ C) of a parallelogram which are equal and the other two angles are acute angles. Hence, we can say that a parallelogram has two Obtuse Angles.

Note:
You can use a protractor to check that the measure of the obtuse angles of a parallelogram. Note that the obtuse angle is greater than 90° and the acute angle is less than 90°. You must draw the figure to represent the obtuse angles in the answer.