Question

How can one calculate the buoyant force of a floating object?

Answer 1

Hint: We know that a buoyant force is caused in response to the weight of an object immersed in a fluid, which results in a partial displacement of the fluid. We also know that buoyancy is a consequence of the Archimedes’ principle. Try and recall the definition of the principle to arrive at a clue in finding an appropriate way to measure the buoyant force acting on a floating object. Remember that for an object to float, its density must be less than that of the fluid.

Formula Used:
Archimedes principle: $F_{buoyant} = W_{fluid\;displaced}$

Complete Solution:
Let us begin by first understanding what a buoyant force means and how it leads to the Archimedes’ principle, which is essentially a tool that we can employ to subsequently determine the buoyant force acting on a floating object.

A buoyant force simply defined, is a force that causes objects to float when suspended in a fluid. It is basically an upward force or an upthrust exerted by the fluid in which it is suspended, in response to the weight exerted on the fluid by the object. This results in a part of the fluid being displaced to accommodate the weight exerted by the object. An object sinks if its material density is more than that of the fluid in which it is suspended and it floats if its density is lesser than that of the fluid. It gets just submerged under the surface of the fluid if the object and the fluid are of equal densities but here, we only consider the case where the object floats ($\rho_{object}<\rho_{fluid}$).

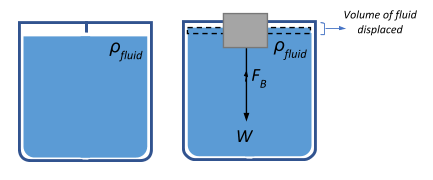
Now, Archimedes’ principle states that the upthrust or the buoyant force exerted on an object partially or completely immersed in a fluid is directly proportional to the weight of the fluid that object displaces.
$\Rightarrow F_{buoyant} = W_{fluid} $
We know that the weight of the fluid is nothing but $W_{fluid} = m_{fluid} \times g$, where $m_{fluid}$ is the mass of the fluid displaced and g is the acceleration due to gravity.

Now, the mass of the fluid can be given in terms of the density of the fluid $\rho_{fluid}$ and the volume of the fluid displaced $V_{displaced}$, both of which are known or easily measurable quantities. They are related as:
$m_{fluid} = \rho_{fluid} \times V_{displaced}$

Therefore,
$ F_{buoyant} = W_{fluid} = m_{fluid} \times g = \rho_{fluid} \times V_{displaced} \times g$

Thus, if we are able to measure the volume of the fluid displaced by the floating object, determining the buoyant force is pretty straightforward as a consequence of the Archimedes’ principle.

Note:
Remember that the magnitude of buoyant force can be derived by calculating the volume of the fluid displaced, though buoyancy is a characteristic of the fluid (and not the immersed object), and is directly proportional to the density of the fluid. Thus, irrespective of our knowledge of the characteristics of the floating object, we can remarkably determine the buoyant force acting on the object.