Question

One end of a rope of length \[5\] meter is tightly tied to the top of a vertical pole and its other end is tied to the horizontal ground. If the rope makes an angle ${30^0}$ to the horizontal then what is the height of the pole?

Answer 1

Hint: If we simply imagine the given situation, the rope forms a triangle (right triangle, see fig) with the pole and ground and draw the figure in which, \[OH\] represents ground, \[OP\] represents the height of pole which is \[h\] & rope represents the hypotenuse of this triangle.
So we can use Pythagoras theorem to solve this problem. Which states that
Square of the hypotenuse=sum of the square of the other two sides.
we also have to know about the trigonometric ratio of them.
After drawing the figure we have to put the relations and values of known things accordingly to calculate the desired value.

Complete step by step solution:
Let us first draw the triangle considering the rope as hypotenuse, the pole as altitude, and the horizontal ground as base.
Length of rope \[ = {\text{ }}5{\text{ }}m\]
Let the length of base be \[OH\]
let the height of the pole \[OP\] be \[h\]
\[HP\] is the rope

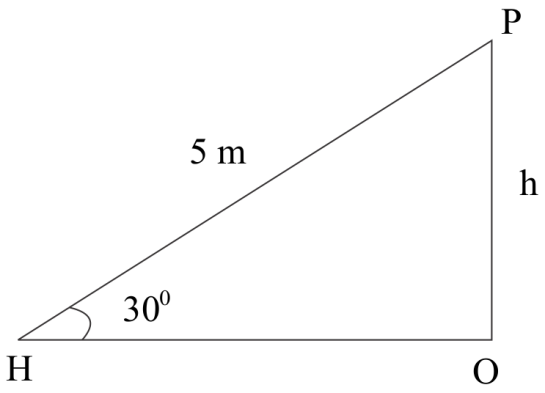
The rope makes an angle of \[30^\circ \] with the base ground \[OH\].
From the triangle applying the relation between an angle and the corresponding sides, we can calculate the base and height measurement easily.
Applying the theorem, from triangle \[OHP\], altitude/hypotenuse \[ = {\text{ }}sin{\text{ }}30^\circ \]
$\Delta OHP,\dfrac{{OP}}{{HP}} = \sin {30^0}$
We will put the value of \[sin{\text{ }}30^\circ \] here, and also put the value of \[HP\].
Putting the values we get,
$ \Rightarrow \dfrac{h}{5} = \dfrac{1}{2}{\text{ }}\left[ {\sin {{30}^0} = \dfrac{1}{2}} \right]$
$ \Rightarrow h = \dfrac{5}{2}{\text{ m}}$
So the height of the pole is \[2.5{\text{ }}m\].


Note: To solve such questions of this topic trigonometry we simply need to imagine the given situation and accordingly draw the figure to understand the problem. After drawing the figure it will be very easy to analyze any problem and then to solve it. We also have to know the values of sin, cos, and tan for various angles \[30^\circ ,{\text{ }}45^\circ ,90^\circ {\text{ }}etc\].