
One mole of an ideal monatomic gas is taken round the cyclic process ABCA as shown in figure. Calculate –
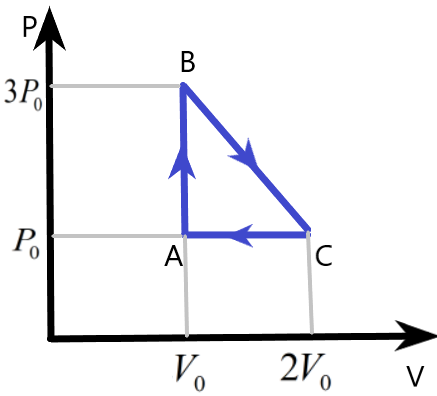
(a) The work done by the gas
(b) The heat rejected by the gas in the path CA and the heat absorbed by the gas in the path AB.
(c) The net heat absorbed by the gas in the path BC.

Answer
546.3k+ views
Hint: We need to understand the relation between the pressure and volume variation in a cyclic process of a monatomic gases with the heat absorption and the heat rejection of the system and the net work done in order to solve this problem.
Complete answer:
We are given a cyclic process of an ideal monatomic gas with the help of a diagram. The pressure and volume variation of the system is plotted which can be used to find the other parameters involved in this system during the process.
We know that the work done by the gas in the cyclic process can be easily found by finding the area under the pressure – volume curve of the process. Here, the area of the triangle ABC will give us the work done W, as –
\[\begin{align}
& W=\text{Area of }\Delta \text{ABC} \\
& \Rightarrow W=\dfrac{1}{2}\times AB\times AC \\
& \Rightarrow W=\dfrac{1}{2}\times \left( 3{{P}_{0}}-{{P}_{0}} \right)\times \left( 2{{V}_{0}}-{{V}_{0}} \right) \\
& \therefore W={{P}_{0}}{{V}_{0}} \\
\end{align}\]
Now, we can find the heat rejected by the process in CA as –
\[\begin{align}
& {{Q}_{CA}}=n{{C}_{P}}\Delta T \\
& \Rightarrow {{Q}_{CA}}=n\left( \dfrac{5}{2}R \right)\Delta T \\
& \Rightarrow {{Q}_{CA}}=\left( \dfrac{5}{2} \right)\left( {{P}_{A}}{{V}_{A}}-{{P}_{C}}{{V}_{C}} \right)\text{ }\because PV=nRT \\
& \Rightarrow {{Q}_{CA}}=\dfrac{5}{2}R\left( {{P}_{0}}{{V}_{0}}-{{P}_{0}}2{{V}_{0}} \right) \\
& \therefore {{Q}_{CA}}=-\dfrac{5}{2}{{P}_{0}}{{V}_{0}} \\
\end{align}\]
Also, the heat absorbed by the process along AB is given similarly as –
\[\begin{align}
& {{Q}_{AB}}=n{{C}_{V}}\Delta T \\
& \Rightarrow {{Q}_{AB}}=n\left( \dfrac{3}{2}R \right)\Delta T \\
& \Rightarrow {{Q}_{AB}}=\left( \dfrac{3}{2} \right)\left( {{P}_{B}}{{V}_{B}}-{{P}_{A}}{{V}_{A}} \right)\text{ }\because PV=nRT \\
& \Rightarrow {{Q}_{AB}}=\dfrac{3}{2}R\left( 3{{P}_{0}}{{V}_{0}}-{{P}_{0}}{{V}_{0}} \right) \\
& \therefore {{Q}_{AB}}=3{{P}_{0}}{{V}_{0}} \\
\end{align}\]
Now, the net heat absorbed by the gas along BC is the work done by the gas along the path, which is the area under the line BC.
\[\begin{align}
& {{Q}_{BC}}={{W}_{BC}}=\text{Area under BC} \\
& \Rightarrow {{\text{W}}_{BC}}=\left( 2{{V}_{0}}-{{V}_{0}} \right)\times \left( 3{{P}_{0}}-{{P}_{0}} \right) \\
& \therefore {{W}_{BC}}=2{{P}_{0}}{{V}_{0}} \\
\end{align}\]
These are the required solutions for the given problem –
(a) \[W={{P}_{0}}{{V}_{0}}\]
(b) \[{{Q}_{CA}}=-\dfrac{5}{2}{{P}_{0}}{{V}_{0}}\]
\[{{Q}_{AB}}=3{{P}_{0}}{{V}_{0}}\]
(c) \[{{W}_{BC}}=2{{P}_{0}}{{V}_{0}}\]
This is the required solution.
Note:
The pressure and volume variation for an ideal gas at a constant temperature is dependent on each other as given by Boyle's law. The pressure exerted by the gas is inversely proportional to the volume occupied of the gas according to this law.
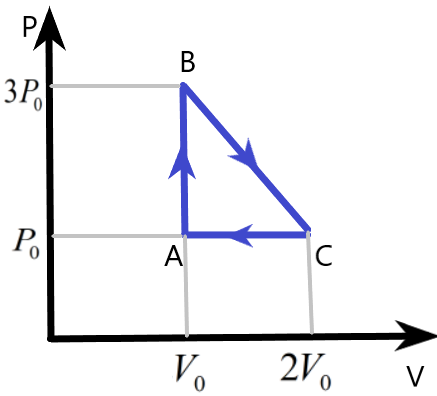
Complete answer:
We are given a cyclic process of an ideal monatomic gas with the help of a diagram. The pressure and volume variation of the system is plotted which can be used to find the other parameters involved in this system during the process.

We know that the work done by the gas in the cyclic process can be easily found by finding the area under the pressure – volume curve of the process. Here, the area of the triangle ABC will give us the work done W, as –
\[\begin{align}
& W=\text{Area of }\Delta \text{ABC} \\
& \Rightarrow W=\dfrac{1}{2}\times AB\times AC \\
& \Rightarrow W=\dfrac{1}{2}\times \left( 3{{P}_{0}}-{{P}_{0}} \right)\times \left( 2{{V}_{0}}-{{V}_{0}} \right) \\
& \therefore W={{P}_{0}}{{V}_{0}} \\
\end{align}\]
Now, we can find the heat rejected by the process in CA as –
\[\begin{align}
& {{Q}_{CA}}=n{{C}_{P}}\Delta T \\
& \Rightarrow {{Q}_{CA}}=n\left( \dfrac{5}{2}R \right)\Delta T \\
& \Rightarrow {{Q}_{CA}}=\left( \dfrac{5}{2} \right)\left( {{P}_{A}}{{V}_{A}}-{{P}_{C}}{{V}_{C}} \right)\text{ }\because PV=nRT \\
& \Rightarrow {{Q}_{CA}}=\dfrac{5}{2}R\left( {{P}_{0}}{{V}_{0}}-{{P}_{0}}2{{V}_{0}} \right) \\
& \therefore {{Q}_{CA}}=-\dfrac{5}{2}{{P}_{0}}{{V}_{0}} \\
\end{align}\]
Also, the heat absorbed by the process along AB is given similarly as –
\[\begin{align}
& {{Q}_{AB}}=n{{C}_{V}}\Delta T \\
& \Rightarrow {{Q}_{AB}}=n\left( \dfrac{3}{2}R \right)\Delta T \\
& \Rightarrow {{Q}_{AB}}=\left( \dfrac{3}{2} \right)\left( {{P}_{B}}{{V}_{B}}-{{P}_{A}}{{V}_{A}} \right)\text{ }\because PV=nRT \\
& \Rightarrow {{Q}_{AB}}=\dfrac{3}{2}R\left( 3{{P}_{0}}{{V}_{0}}-{{P}_{0}}{{V}_{0}} \right) \\
& \therefore {{Q}_{AB}}=3{{P}_{0}}{{V}_{0}} \\
\end{align}\]
Now, the net heat absorbed by the gas along BC is the work done by the gas along the path, which is the area under the line BC.
\[\begin{align}
& {{Q}_{BC}}={{W}_{BC}}=\text{Area under BC} \\
& \Rightarrow {{\text{W}}_{BC}}=\left( 2{{V}_{0}}-{{V}_{0}} \right)\times \left( 3{{P}_{0}}-{{P}_{0}} \right) \\
& \therefore {{W}_{BC}}=2{{P}_{0}}{{V}_{0}} \\
\end{align}\]
These are the required solutions for the given problem –
(a) \[W={{P}_{0}}{{V}_{0}}\]
(b) \[{{Q}_{CA}}=-\dfrac{5}{2}{{P}_{0}}{{V}_{0}}\]
\[{{Q}_{AB}}=3{{P}_{0}}{{V}_{0}}\]
(c) \[{{W}_{BC}}=2{{P}_{0}}{{V}_{0}}\]
This is the required solution.
Note:
The pressure and volume variation for an ideal gas at a constant temperature is dependent on each other as given by Boyle's law. The pressure exerted by the gas is inversely proportional to the volume occupied of the gas according to this law.
Recently Updated Pages
The number of solutions in x in 02pi for which sqrt class 12 maths CBSE

Write any two methods of preparation of phenol Give class 12 chemistry CBSE

Differentiate between action potential and resting class 12 biology CBSE

Two plane mirrors arranged at right angles to each class 12 physics CBSE

Which of the following molecules is are chiral A I class 12 chemistry CBSE

Name different types of neurons and give one function class 12 biology CBSE

Trending doubts
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Explain zero factorial class 11 maths CBSE

What is 1s 2s 2p 3s 3p class 11 chemistry CBSE

Discuss the various forms of bacteria class 11 biology CBSE

State the laws of reflection of light

An example of chemosynthetic bacteria is A E coli B class 11 biology CBSE




