Question

One of the equal sides of an isosceles triangle is 13 cm and the perimeter is 50 cm. Find the area of the triangle in $c{m^2}.$

Answer 1

Hint: To find the area of the triangle we need to gather information like height of the triangle base of the triangle and then we can put them directly into the formula to find the answer.

Complete step-by-step solution:
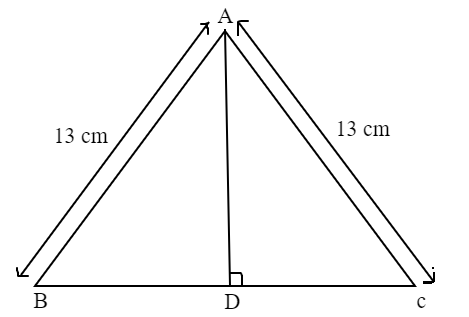
Let ABC be the triangle whose sides AB=AC because it is an isosceles triangle.
Therefore, AB=AC=13cm
It is given that the perimeter of the triangle is 50cm.
So, the third side of triangle is
BC=50-13-13=24cm
Since, AD is the perpendicular bisector of BC
$BD = DC = \dfrac{{24}}{2} = 12cm$
 In right $\Delta ABD,$ using Pythagoras Theorem
$
A{B^2} = A{D^2} + B{D^2} \\
   \Rightarrow {13^2} = A{D^2} + {12^2} \\
   \Rightarrow 169 = {AD}^{2} + 144 \\
   \Rightarrow {AD}^{2} = 25 \\
   \Rightarrow AD = 5cm \\
 $
Now, area of $\Delta ABC $
$
   = \dfrac{1}{2} \times Base \times Altitude \\
   = \dfrac{1}{2} \times BC \times AD \\
   = \dfrac{1}{2} \times 24 \times 5 = 60 c{m^2} \\
$
Hence, the area of the triangle is $60 c{m^2}.$

Note: In order to solve this type of questions, remember the formula of area of the triangle and some properties and theorems of the triangle such as Pythagoras theorem. Also remember a line bisector divides the in line two equal parts and the line bisector is perpendicular to the line. Also when all sides of a triangle are known, the area of the triangle can also be found using Heron's formula.