Question

What is one proof of the converse of the Isosceles Triangle Theorem?

Answer 1

Hint: To solve this question we need to have the knowledge of the Isosceles Triangle Theorem. To prove this we will have to construct a line which bisects the angle of the triangle which meets the opposite side. We will analyse the triangle and will apply the property of the congruency in the two triangles which formed due to the angle bisector.

Complete step by step answer:
The question asks to prove the converse of the Isosceles Triangle Theorem. Isosceles triangle is that kind of triangle which has two equal sides. The Converse of Isosceles Triangle theorem states that if two angle$\angle ABC$ (angle B) and $\angle ACD$ (Angle C) are congruent in a triangle $\vartriangle ABC$ then the side corresponding to it is also congruent or equal.
Let us prove the following with the given using the following steps:
Firstly we will take a triangle namely ABC with equal angles which are$\angle ABC$ (angle B) and $\angle ACD$ (Angle C) as given below:

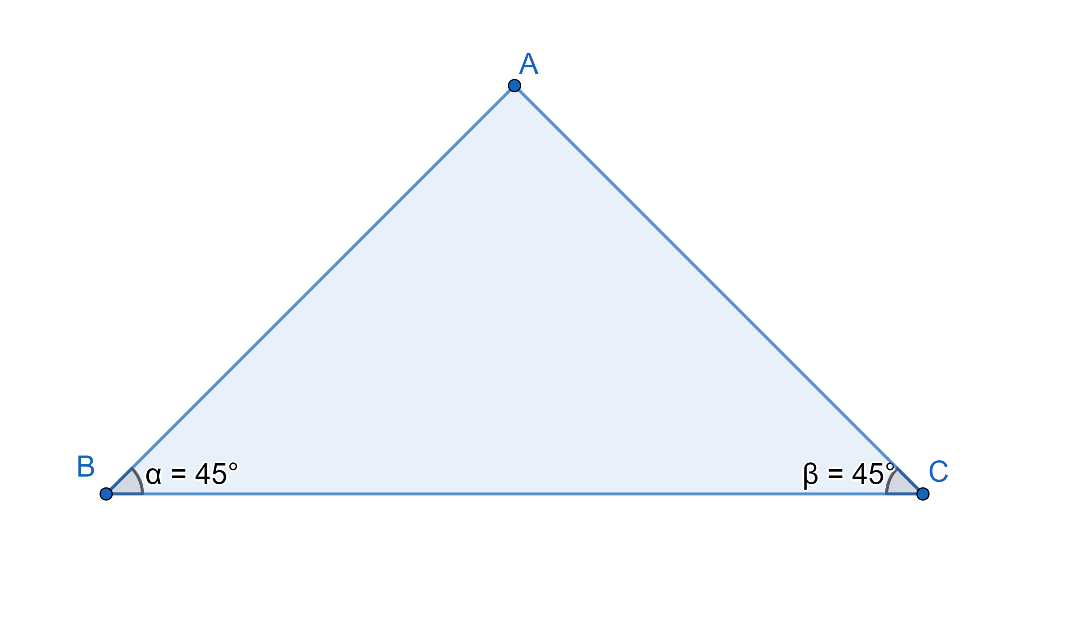
We will now draw a bisector of $\angle BAC$ which will divide the angle of A into two equal parts which meets the opposite side $BC$ at point D. On doing this the triangle looks same as given below:

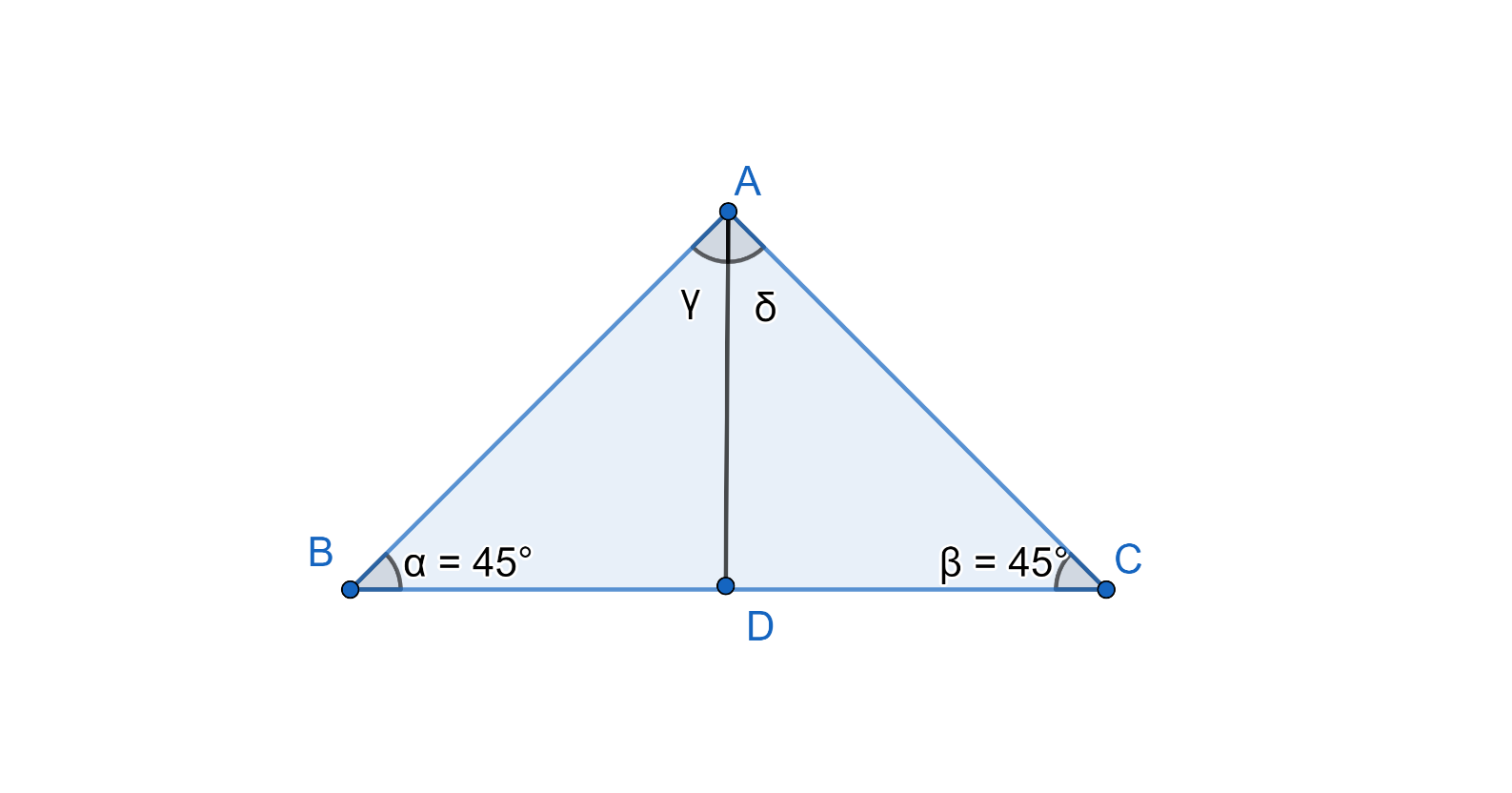
Now, on analysing the above triangle we see that the triangle could be proved congruent. The three properties which make the triangle $\vartriangle ABD$ and $\vartriangle ACD$ congruent are
$\left( i \right)\angle ABD=\angle ACD$
These angles are equal as stated in the theorem.
$\left( ii \right)\angle BAD=\angle CAD$
These two angles are equal because the line $AD$ which was constructed is a bisector of the angle $\angle BAC$.
$\left( iii \right)AD=AD$
In both the triangles $\vartriangle ABD$ and $\vartriangle ACD$ the line segment $AD$ which is also the angle bisector of $\angle A$ is common.
So by the$AAS$ property of triangle the two triangle $\vartriangle ABD$ and $\vartriangle ACD$ are congruent.
Since corresponding part of congruent triangles are congruent, so the two sides of the triangle will be equal, which is
$AB=AC$
$\therefore $ proved the converse Isosceles Triangle Theorem.

Note: In isosceles triangle the two sides are equal and the two angles corresponding to the sides are equal. The angle bisector divides the unequal angle into equal half. The angle bisector of the triangle is perpendicular to the side with different length.