Question

Only the current inside the Amperian loop contributes in
A. Finding a magnetic field at any point on the Amperian loop.
B. Line integral of Magnetic field
C. In both of the above
D. In neither of them

Answer 1

Hint: As we all know that the spinning motion and the orbiting motion of the nucleus produces a magnetic field whenever the current passes through a wire. Basically when the current flows the electric charge is in motion.

Complete step by step answer:
We can refer to the below figure for better understanding.

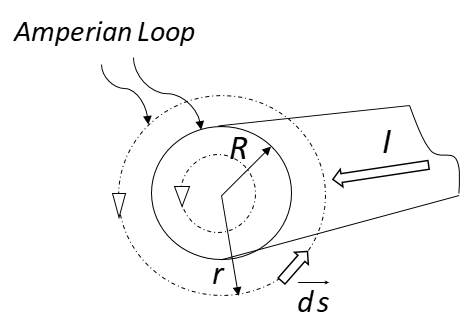
In the above figure, the current I is flowing in a conductor of radius R, and the ampere loop is of radius r is considered by an imaginary loop perpendicular to the plane of I.
We can suppose if there is a current distribution $I_1$, then the magnetic field around the distribution can be found out by using ampere’s law by taking a symmetrical ampere loop around the distribution $I_1$. But suppose that if there is another distribution $I_2$, somewhere around $I_1$ the net magnetic at a point on the ampere loop around $I_1$ is the resultant of both the effects of $I_1$ and $I_2$. So we can say that the magnetic field on the ampere loop depends upon all the currents distributions present around. So only the current inside the ampere loop does not contribute to finding a magnetic field on any point on the ampere loop. Hence option (A) is wrong.
If we look at option (B), then it is the definition of ampere’s law i.e. only the current inside the ampere loop contributes to the line integral of the magnetic field.
We can express the relation for ampere’s law as:
$\oint {\overrightarrow B \times dl} = {\mu _0}{I_{in}}$
Here B is the magnetic field generated, dl is the elemental length element of the conductor, ${\mu _0}$ is the permeability of free space and Iin is the enclosed current.

Therefore, we can say that the correct option is (B).

Note:
Here we should note that the choice of the Ampere loop is the most important. The Amperian loop must be selected in such a way that all points in the ampere loop the magnitude of magnetic field B are constant and the plane of the magnetic field and the direction of current are perpendicular to each other.