Question

How many orbitals make up the $4d$ subshell?

Answer 1

Hint: Here in $4d$ subshell number $4$ is the value of principal quantum number while d is here the azimuthal quantum number so the orbitals will be the same as an ordinary d-orbital makes. The number of orbital is the blocks that you made to represent it, like in s orbital we have to make only one block hence it will have one orbital similarly in p orbital there are three blocks made hence it will have three orbitals.

Complete step-by-step answer:
To represent any shell and its inner subshell we have four quantum numbers which by numbers sketch the naming of orbitals they contain. As we know for s orbital value $1\,s$ here $1$ is the principal quantum number the value of the main shell in which the electron exists. Now how to calculate the value for azimuthal quantum number? We can write it from $0$ to $(n - 1)$ it means we can write it in terms of a formula like,
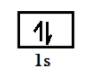
$l\, = \,0\,\,to\,(n - 1)$ so for $1\,s$ we have $n = 1$ so if we put her the value of n we get $l = 0$ , therefore it is represented by one box or orbital having value of magnetic quantum number as ${m_l}\, = \, - l\,\,to\, + l\,$ so we get value zero. It can be represented as in figure and have two electrons of magnetic spin quantum number as $\left( { + \dfrac{1}{2}} \right)\,and\,\left( { - \dfrac{1}{2}} \right)$

Now for our question $4d$ has value of principal quantum number as $n = 4$ so if we try to calculate the value of azimuthal quantum number, it will be
 $l\, = \,0\,\,to\,(n - 1)$
$l\, = \,0\,\,to\,(4 - 1)\, = \,0,1,2,3$

Among which $l = 2$ is for d orbital hence the value of magnetic quantum number is from ${m_l}\, = \, - l\,\,to\, + l\,$= ${m_l}\, = \,( - 2)\,\,to\,( + 2)$ = $ - 2,\, - 1,\,0,\, + 1,\, + 2$

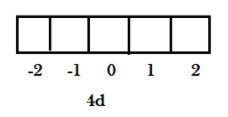
Now we can say that $4d$ has five orbitals having magnetic quantum numbers from $( - 2)\,\,to\,( + 2)$ .

Note: The principal quantum number and azimuthal quantum number both give the value of all possible numbers of subshells which that principle quantum number can accommodate, we can find the subshell using the nomenclature.
$l = 0\, \to s$
$l = 1 \to p$
$l = 2\, \to d.......so\,on$