Question

What is the packing efficiency of a BCC unit cell.

Answer 1

Hint: The packing efficiency of a body centred cubic unit cell is calculated by the presence of atoms in the respective unit cell and how much space it can acquire. It is calculated in percentile form.

Complete step by step solution:
Let us start by understanding the concepts of crystal lattice and the packings.
Crystal lattice- It is the arrangement of atoms, molecules or ions of a crystal in the form of space lattice.
Unit cell- It is the smallest repeating pattern of a unit which forms a crystal structure. It is a representation of a crystal on a microscopic scale. There are three types of unit cells i.e. simple cubic structure, face centred structure and body centred structure.
1. Simple/primitive cubic unit cell- Here, the atoms are present only at the corners of the cube i.e. it would consist of only one atom in total as eight proportions of a sphere will occupy eight corners.
2. Face centred cubic unit cell- Here, the atoms are present at the corners of the cube and also to the faces of the cube. Thus, there will be four atoms in total for the FCC unit cell. One atom from the corners of the cell and other three will be from the faces of the cube as each face will comprise half the sphere.
3. Body centred cubic unit cell- Here, the atoms are present at the corners of the cube and also one in the centre of the cube. Thus, there are two atoms in total for a BCC unit cell.

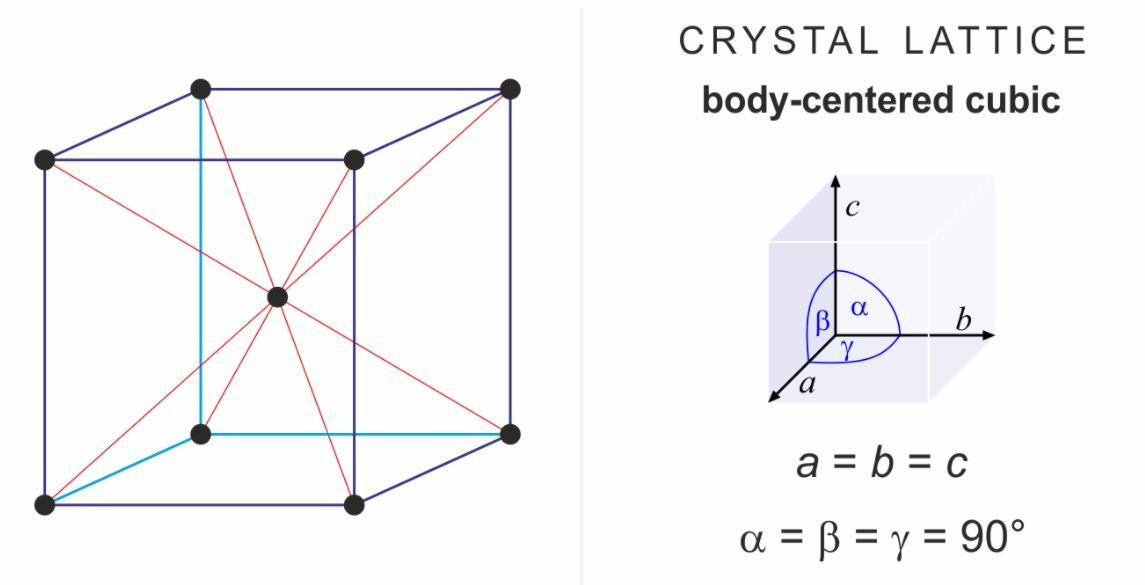
Now, let us discuss the packing efficiency of BCC;
Packing efficiency is the fraction of the unit cell actually occupied by the atoms. It is given as,
Packing efficiency = $\dfrac{{{V}_{a}}}{{{V}_{c}}}\times 100$
where,
${{V}_{a}}$ = Volume occupied by the atoms
${{V}_{c}}$ = Volume of unit cell.
For BCC,
The relationship between the edge length a and radius r of the unit cell is,
\[a=\dfrac{4r}{\sqrt{3}}\]
The volume of the unit cell is given as.
\[{{a}^{3}}={{\left( \dfrac{4r}{\sqrt{3}} \right)}^{3}}=\dfrac{64{{r}^{3}}}{3\sqrt{3}}\]
The volume occupied by one atom is $\dfrac{4}{3}\pi {{r}^{3}}$
As BCC has two atoms, thus the volume for two atoms is,
\[2\times \dfrac{4}{3}\pi {{r}^{3}}=\dfrac{8}{3}\pi {{r}^{3}}\]
Thus, the packing efficiency for BCC is given as,
Packing efficiency = $\dfrac{\dfrac{8}{3}\pi {{r}^{3}}}{\dfrac{64{{r}^{3}}}{3\sqrt{3}}}\times 100=68.04%$

Therefore, packing efficiency of BCC is 68.04%.

Note: Do note that the packing efficiency of any unit cell will always be less than 100% always. This truly depends on the number of atoms present in the structure.