Question

What is the path followed by a moving body on which a constant force acts in a direction other than initial velocity (i.e. excluding parallel and antiparallel direction)?
(A). Straight lie
(B). Parabolic
(C). Circular
(D). Elliptical

Answer 1

Hint: The motion of a body is the resultant of one or more forces acting on it. In a projectile motion, the body has motion in horizontal as well as vertical direction. Resolving the velocity into its components and applying equation of motion, we can determine the path followed by the body

Formula used:
$x=u\cos \theta t$
$s=ut+\dfrac{1}{2}a{{t}^{2}}$

Complete step-by-step solution:
According to Newton’s second law, a body undergoes acceleration when a force acts on it, therefore,
$F=ma$
Here, $F$ is the force acting on a body
$m$ is the mass of a body
$a$ is the acceleration of the body

In a projectile, the path followed by the body is given as

Here $u$ is the initial velocity of the body. The force acting on the body should not be parallel or anti-parallel, let $\phi $ be the angle between initial velocity and force, then, $\phi \ne 0$ or $\phi \ne {{180}^{o}}$

In a projectile no force is acting in the horizontal motion therefore, the horizontal velocity remains constant. In the vertical direction, the force of gravity acts on the body hence, the acceleration is constant. The FBD diagram of the body in projectile motion is

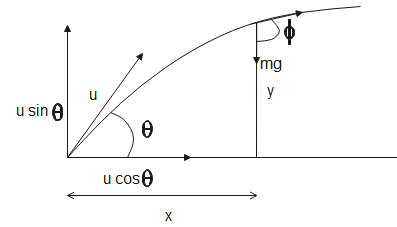
The force acting on the particle is $mg$ and acceleration in the vertical direction is equal to g.

Let x be the distance covered along the horizontal axis, then
$x=u\cos \theta t$ - (1)

Let y be the distance covered along the vertical axis. Applying equation of motion along vertical axis we get,
$s=ut+\dfrac{1}{2}a{{t}^{2}}$
Here, $s$ is the distance covered
$t$ is the time taken
$a$ is acceleration

Substituting given values in the above equation,
$y=u\sin \theta t-\dfrac{1}{2}g{{t}^{2}}$
Substituting $t$ from eq (1)
$\begin{align}
  & y=u\sin \theta \dfrac{x}{u\cos \theta }-\dfrac{1}{2}g{{\left( \dfrac{x}{u\cos \theta } \right)}^{2}} \\
 & \Rightarrow y=x\tan \theta -\dfrac{1}{2}g\dfrac{{{x}^{2}}}{{{u}^{2}}{{\cos }^{2}}\theta } \\
\end{align}$
The above equation represents the equation of a parabola.

Therefore, in projectile motion, the force acting on the body is not in the direction of initial velocity and the path followed is a parabola.

Hence, the correct option is (B).

Note:
Since the force is constant, acceleration is also constant. The velocity becomes zero at the highest point of the projectile and it is maximum at the lowest point. The velocity and force are not in the same direction at any point of the projectile. The force of gravity or mg is responsible for decelerating the body.