Question

What is the perimeter of the track, in meters? Assume that $ \pi = 3.14 $ and round to the nearest hundredth of a meter?

Answer 1

Hint: Here first of all we will redraw the figure and make the three parts of the given figure and entitle them. We will observe the figure properly which suggests that there are two semicircles and one rectangle. Use the standard formula for the perimeter which is the outer length of the closed figure and find the resultant required value.

Complete step-by-step answer:

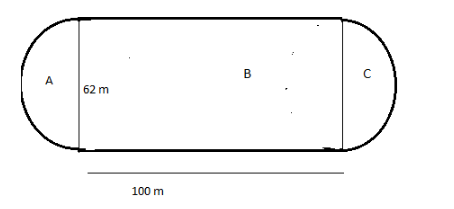
Perimeter for part A:
Part A is the semicircle, since the diameter of the semicircle is given $ 62m $
Therefore, radius $ r = \dfrac{d}{2} $
Place the value in the above equation
 $ r = \dfrac{{62}}{2} $
Common factors from the numerator to the denominator cancel each other.
 $ \Rightarrow r = 31\;m $
Now, perimeter of semicircle is $ = \pi r $
Place the values in the above equation-
p $ = (3.14)(31) $
Simplify the above equation-
P $ = 97.34 $ m
Since perimeter is the sum of all the sides of the closed figure,
Perimeter of the above track is equal to –
P $ = 97.34 + 97.34 - 62 - 62 + 100 + 100 $
Simplify the above equation-
P $ = 194.68 + 200 - 124 $
Simplify the above equation –
Perimeter, P $ = 270.68\;m $
This is the required solution.
So, the correct answer is “ P $ = 270.68\;m $ ”.

Note: Here we have subtracted the base of the semicircle since it is not included in the circumference. Do not forget to write the appropriate units after the solution. Know the difference between the area and circumference of the rectangle. Area is represented in square units and it is the product of two adjacent sides whereas the circumference is the sum of all the four sides of the rectangle.