Question

What is the phase angle in a series RLC circuit at resonance?
A) ${180^0}$
B) ${90^0}$
C) ${0^0}$
D) $ - {90^0}$
E) None of the above

Answer 1

Hint: A series RLC is an AC circuit that is said to be in electrical resonance when the circuit power factor is unity i.e., ${X_L} = {X_C}$. Where ${X_L}$ and ${X_C}$ are inductive reactance and capacitive reactance respectively.
The phase angle in a RLC circuit is given by $\phi = {\tan ^{ - 1}}\left( {\dfrac{{{X_L} - {X_C}}}{R}} \right)$. Where $R$ is the resistance.

Complete step by step answer:
Let’s draw an AC circuit containing resistor, inductor and capacitor in series. $E$ and $I$ are the e.m.f. and current in the circuit respectively.

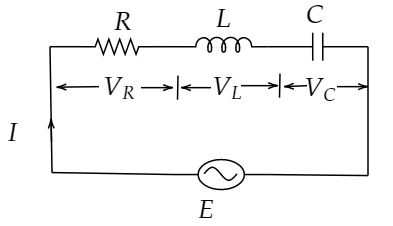
The voltage across resistor $\left( R \right)$, ${V_R} = IR$
${V_R}$ is in phase with $I$.
The voltage across inductor $\left( L \right)$, ${V_L} = I{X_L}$
${V_L}$ leads $I$ by ${90^0}$.
The voltage across capacitor $\left( C \right)$, ${V_C} = I{X_C}$
${V_C}$ lags $I$ by ${90^0}$.
Consider ${V_L} > {V_C}$. Now draw the phasor diagram.

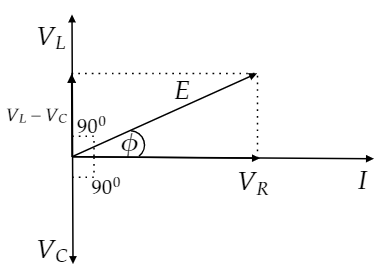
The resultant voltage in the phasor diagram is the applied voltage and it is given by
$E = \sqrt {{V_R}^2 + {{\left( {{V_L} - {V_C}} \right)}^2}} $
Or $E = \sqrt {{{\left( {IR} \right)}^2} + {{\left( {I{X_L} - I{X_C}} \right)}^2}} $
Or $ I = \dfrac{E}{{\sqrt {{R^2} + {{\left( {{X_L} - {X_C}} \right)}^2}} }}$
The quantity $Z = \sqrt {{R^2} + {{\left( {{X_L} - {X_C}} \right)}^2}} $ is called impedance of the circuit.
The angle $\phi $ in the above phasor diagram is known as phase angle in the circuit.
$\tan \phi = \dfrac{{{V_L} - {V_C}}}{{{V_R}}}$
Or $\tan \phi = \dfrac{{{X_L} - {X_C}}}{R}$
Or $ \Rightarrow \phi = {\tan ^{ - 1}}\left( {\dfrac{{{X_L} - {X_C}}}{R}} \right)$
At resonance, the impedance of the circuit is minimum and is equal to the resistance of the circuit.
i.e., $Z = R$
Or $\sqrt {{R^2} + {{\left( {{X_L} - {X_C}} \right)}^2}} = R$
Further simplify
$ \Rightarrow {X_L} = {X_C}$
Now at resonance, phase angle $\phi = {\tan ^{ - 1}}\left( 0 \right)$
Or $\phi = {0^0}$
Hence, the correct option is (C) ${0^0}$.

Note: Alternative method for solving the problem:
When the RLC series AC circuit is at resonance, the average power in the circuit is maximum.
$P = {E_{rms}}{I_{rms}}\cos \phi $.
Where ${E_{rms}}$ and ${I_{rms}}$ are the rms values of voltage and current in the circuit.
$co\phi $ is called the power factor of the circuit.
At resonance, $P = {E_{rms}}{I_{rms}}$
Therefore, $\cos \phi = 1$
Or $\phi = {0^0}$