
How do you plot the equation by plotting point
Answer
459.6k+ views
Hint: In this problem, we have to graph the given equation. We can see that the given equation is a straight-line equation. The equation
Complete step by step answer:
We know that the given linear equation is
We also know that the given equation is a straight line, which is parallel to the y-axis and the line passes through all the points in the plane with an x-coordinate of 2.
We should also know that the equation
We can also plot some points, through which the line passes through.
If we want to plot the points, we will have points where x value is always 2, regardless of the value for y.
We can see that the points
Now we can graph the given line
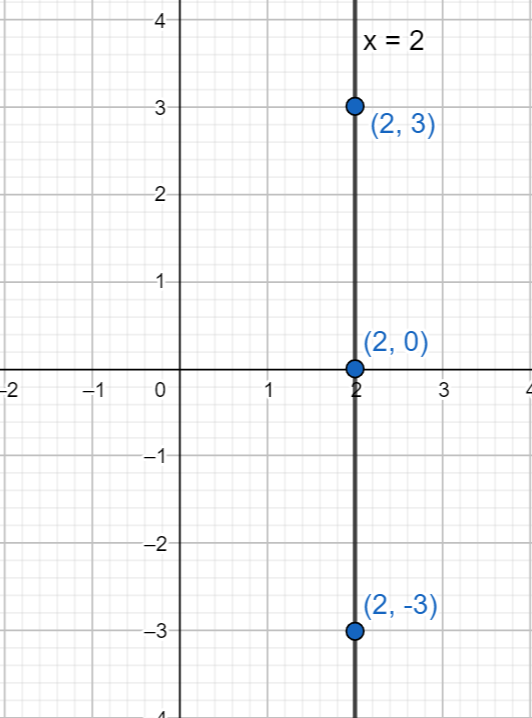
Note: Students make mistakes in understanding the concept of line equation. We should know that to solve these types of problems, we have to understand the concept of line. We should also know that the equation represents a vertical line with only an x-intercept. This line will intersect the x-axis at the point given.
Complete step by step answer:
We know that the given linear equation is
We also know that the given equation is a straight line, which is parallel to the y-axis and the line passes through all the points in the plane with an x-coordinate of 2.
We should also know that the equation
We can also plot some points, through which the line passes through.
If we want to plot the points, we will have points where x value is always 2, regardless of the value for y.
We can see that the points
Now we can graph the given line

Note: Students make mistakes in understanding the concept of line equation. We should know that to solve these types of problems, we have to understand the concept of line. We should also know that the equation represents a vertical line with only an x-intercept. This line will intersect the x-axis at the point given.
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
The singular of lice is louse A Yes B No class 8 english CBSE

How many ounces are in 500 mL class 8 maths CBSE

Summary of the poem Where the Mind is Without Fear class 8 english CBSE

Advantages and disadvantages of science

In Indian rupees 1 trillion is equal to how many c class 8 maths CBSE

What led to the incident of Bloody Sunday in Russia class 8 social science CBSE





