Question

Plot the graph of ${{\cos }^{-1}}\left( \cos x \right)$ and write its domain and range.

Answer 1

Hint: In this question, we will first understand the relation of $\cos x$ and ${{\cos }^{-1}}x$. Then, observe the graph of $\cos x$, and how they change sign and use it to plot a graph of ${{\cos }^{-1}}\left( \cos x \right)$. From the graph, we will find its range and domain.


Complete step-by-step answer:

Firstly, let us understand what is meant by the inverse function of cosine.
Suppose, $y={{\cos }^{-1}}x$.
Then, for each value of $x$ there will exist some value of $y$. Then, the cosine inverse of this value of $y$ will be $x$.
For example, $\dfrac{1}{2}=\cos \dfrac{\pi }{6}$.
Then, ${{\cos }^{-1}}\dfrac{1}{2}=\dfrac{\pi }{6}$.
Now, $\cos x$ is a periodic function with period $2\pi $, which means its values repeat in the same pattern after $2\pi $ increases in $x$. That is, $\cos x=\cos \left( 2\pi +x \right)$.
Since, $\cos x$ is periodic with period $2\pi $. Therefore, ${{\cos }^{-1}}\left( \cos x \right)$ is also period with period $2\pi $.
Also, the domain here is set of those values of $x$ for which ${{\cos }^{-1}}\left( \cos x \right)$ is defined. And, range is the set of values where ${{\cos }^{-1}}\left( \cos x \right)$ lies.
Now, for all real values of $x$, $\cos x$lies between -1 and 1. And, between -1 and 1, the inverse function of cosine is defined. Therefore, ${{\cos }^{-1}}\left( \cos x \right)$ is defined for all real values of $x$. Hence, the domain of ${{\cos }^{-1}}\left( \cos x \right)$ is $\left( -\infty ,\infty \right)$ .
We know, graph of $y=\cos x$ is:

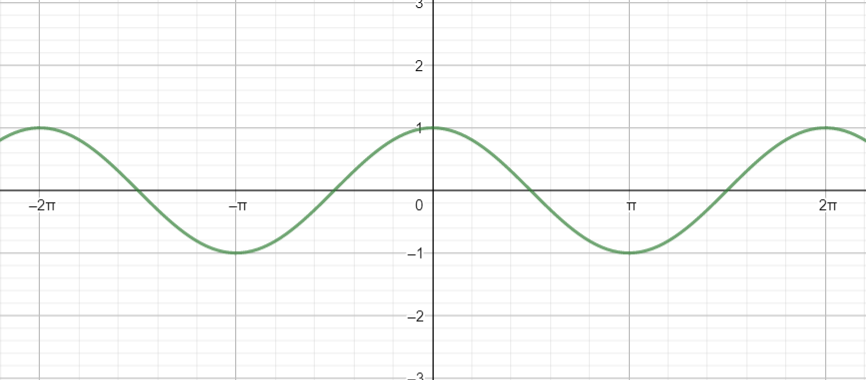
We see that, in the interval $\left[ -\pi ,\pi \right]$, for two different values of $x$, we have the same value of $y$.
Also, from definition of cosine inverse, in this graph, we get,
${{\cos }^{-1}}y=x$
If we substitute $y=\cos x$ here, we get,
${{\cos }^{-1}}\left( \cos x \right)=x$
Now, in graph of ${{\cos }^{-1}}\left( \cos x \right)$, we have,
 $y={{\cos }^{-1}}\left( \cos x \right)$
$\Rightarrow y=x$
But, in interval $\left[ -\pi ,\pi \right]$, for two different values of $x$, we have the same value of $y$.
Let those two different values be represented by ${{y}_{1}},{{y}_{2}}$.
Now, as $x$ increases from $-\pi $ to 0, $\cos x$ increases from -1 to 1, and hence, ${{\cos }^{-1}}\left( \cos x \right)$ decreases from $\pi $ to 0. Therefore, here we will have, ${{y}_{1}}=-x$.
And as $x$ increases from 0 to $\pi $, $\cos x$ decreases from 1 to -1, and hence, ${{\cos }^{-1}}\left( \cos x \right)$ increases from 0 to$\pi $. Therefore, here we will have, ${{y}_{2}}=x$.
Also, from $-\pi $ to $\pi $, length of interval is $2\pi $ and ${{\cos }^{-1}}\left( \cos x \right)$ periodic with period $2\pi $. Therefore, the rest of the graph will repeat the same as in the interval $\left[ -\pi ,\pi \right]$.
Hence, the graph of ${{\cos }^{-1}}\left( \cos x \right)$ is given by:

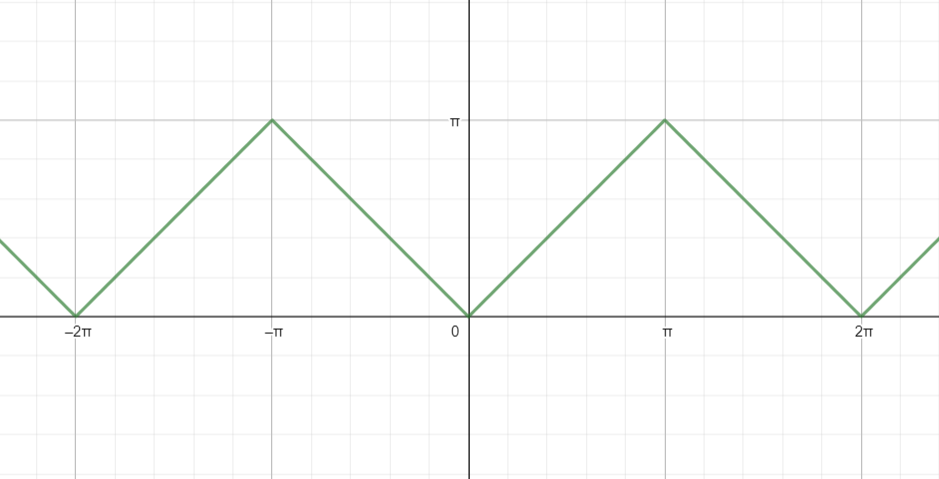
Here, values of ${{\cos }^{-1}}\left( \cos x \right)$ lies between 0 to $\pi $.
Hence for the graph of ${{\cos }^{-1}}\left( \cos x \right)$ plotted above, the domain is $\left( -\infty ,\infty \right)$ and the range is $\left[ 0,\pi \right]$.

Note: While plotting the graph, keep in mind that for two different values of $x$, ${{\cos }^{-1}}\left( \cos x \right)$ will have the same value in interval of length $2\pi $. So, looking at $y=x$, do not directly plot a graph of an infinite straight line.