Question

How do you plot the graph $y = \dfrac{1}{4}x + 2?$

Answer 1

Hint: First find the intercepts of the graph with substituting method that is substitute the values of abscissa and ordinate equals to zero separately in the given equation to get the value of ordinate and abscissa respectively that value is known as $y\;{\text{and}}\;x$ intercepts respectively.
Now plot the coordinates of the intercepts on the graph paper keeping the scale of the graph
accordingly to the coordinates and join the points then extend the produced line segment which will be the required graph for the given equation.

Complete step by step solution:We will first find the $x - y$ intercepts of the graph then plot them on the graph and produce the required graph.
Finding $x$ intercept by putting the value of $y = 0$ in the given equation
$
\Rightarrow y = \dfrac{1}{4}x + 2 \\
\Rightarrow 0 = \dfrac{1}{4}x + 2 \\
\Rightarrow - 2 = \dfrac{1}{4}x \\
\Rightarrow x = - 8 \\
$
Same for $y$ intercept,
$
\Rightarrow y = \dfrac{1}{4}x + 2 \\
\Rightarrow y = \dfrac{1}{4} \times 0 + 2 \\
\Rightarrow y = 2 \\
$
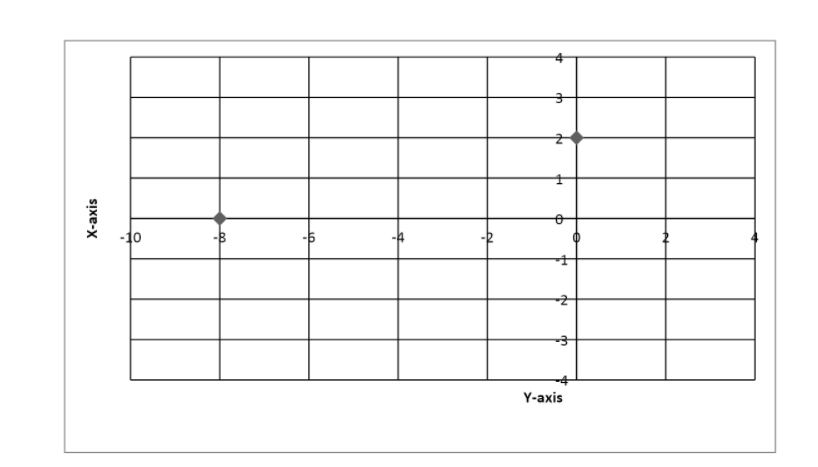
$\therefore $ coordinates of $x\;{\text{and}}\;y$ intercepts are given as $\left( { - 8,\;0}
\right)\;and\;\left( {0,\;2} \right)$ respectively.
Now plotting these coordinates on a graph

Now joining the points and extending the produced line segment in order to get the required graph of the given linear equation.

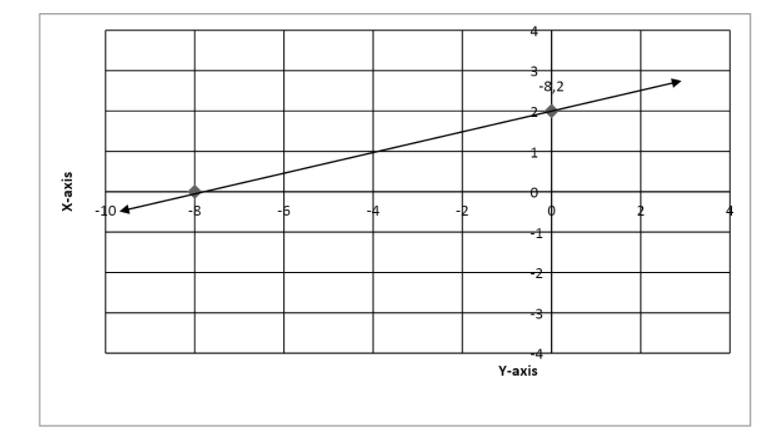
Therefore this is the required graph of the equation $y = \dfrac{1}{4}x + 2$

Note:
On plotting a graph of a linear equation, intercept method is only used when the equation has a constant in it, because if it does not have any constant present in the equation then the line will pass through the origin which means the value of both intercepts equals zero.
Equation having the degree equals to one is known as linear equation and the graph of a linear equation is always a straight line.