Question

Point M is the midpoint of segment AB . If $AB=8$cm find AM. \[\]

Answer 1

Hint: We recall the definition of a line segment and the midpoint of a line segment as the middle point of a line segment. We use the fact that divides the line segment into two equal halves and is equidistant from both endpoints to find AM.

Complete step-by-step solution
We know from geometry that a line segment is a geometrical figure which is part of a straight line and is bounded by two distinct points on the straight line called endpoints and contains every point on the line between its endpoints. If A and B are two distinct points on the line $\overleftrightarrow{PQ}$ then line segment AB is denoted $\overline{AB}$. \[\]

The shortest distance between the two points is called the length of the line segment and is denoted$AB$. The midpoint of the line segment is the middle point of the line segment. The midpoint divides the line segment and divides the line segment into two line segments with equal length. It also means the midpoint is equidistant from both endpoints.\[\]

We are given in the question that point M is the midpoint of segment AB. We are also given the length of the line segment $AB=8$. \[\]
 

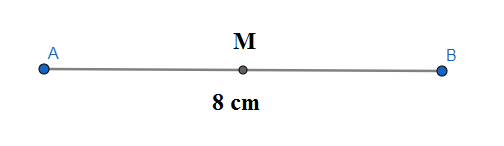
We see that midpoint M has divided $\overline{AB}$ into two line segments$\overline{AM},\overline{MB}$. Since they will be off equal length, we have;
\[AM=MB\]
 We add the lengths of new line segments $\overline{AM},\overline{MB}$ and will get the length of $\overline{AB}$. So we have;
\[\begin{align}
  & AM+MB=AB \\
 & \Rightarrow AM+AM=AB\left( \because AM=BM \right) \\
 & \Rightarrow AM=\dfrac{AB}{2} \\
\end{align}\]
We put $AB=8$cm in the above step to have;
\[AM=\dfrac{8}{2}=4\text{ cm}\]

Note: We note that dividing a geometric figure into two equal halves is called bisection. The line perpendicular to the line segment and passing through the midpoint is called the perpendicular bisector. The midpoint of the diameter of the circle is called the center. We can find the point using construction by taking arcs of length equal to the length of line segments.