Question

What is the power of a lens? What is the SI unit? Name the type of lens whose power is negative.
The image of an object formed by a lens is real, inverted and of the same size as the object. If the image is at a distance of \[40cm\] from the lens, what is the nature and power of the lens? Draw a ray diagram to justify your answer.

Answer 1

Hint: We are asked to define the power of a lens and find the power and nature of the lens. We start by defining power and identifying the lens with negative power. Then we gather all the information given in the question. We apply the formulas and get the value of focal length and find the reciprocal of it to get the power of the given lens.

Formulas used:
The formula for finding the power of a given lens is,
\[P = \dfrac{1}{f}\]
The formula used to find the focal length of a lens is,
\[\dfrac{1}{f} = \dfrac{1}{v} - \dfrac{1}{u}\]
The magnification is given by the formula,
\[m = \dfrac{u}{v}\]
Where \[v\] is the distance from the lens to the image and \[u\] is the distance from the object to the lens.

Complete answer:
Power of a lens is defined as the reciprocal of its focal length. The SI unit of power is Diopter, it is represented by D. Moving onto the second part, we know that the focal length is the reciprocal of power. If the power of a lens is negative, its focal length must be negative as well. Now we can approach this with respect to the focal length. The focal length of the diverging lens is negative. Concave lens is a diverging lens, hence it has negative power.

The following information is given, the distance from the lens at which the object is placed is, \[u = - 40\,cm\]. It is said that the magnification of the image is one (same size) and the fact that the image is inverted gives us the sign of magnification as negative.

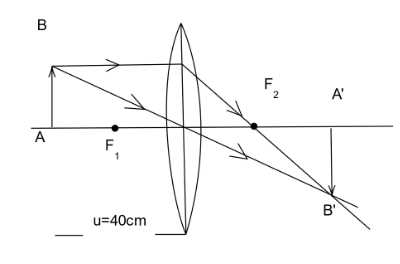
Now with this information we find the image distance,
\[v = \dfrac{u}{m} \\
\Rightarrow v= \dfrac{{ - 40}}{{ - 1}} \\
\Rightarrow v= + 40\,cm\]
We use the formula to find the focal length to get,
\[f = \dfrac{{uv}}{{u - v}} \\
\Rightarrow f= \dfrac{{ - 40 \times 40}}{{ - 40 - 40}} \\
\Rightarrow f= \dfrac{{ - 1600}}{{ - 80}} \\
\Rightarrow f= 20\,cm\]
Now to find the power of this lens, we find the reciprocal and get
\[P = \dfrac{1}{f} \\
\Rightarrow P= \dfrac{1}{{20}} \\
\therefore P= 50\,D\]

Therefore, the power of the given lens is, \[50\,D\].

Note: The place we used the lens formula can be done in another way. In a diverging lens, when the image distance and the object distance are the same, the image and object is found to be at a distance of \[2F\] . We can find the focal length from this relation as well.