Question

PQ is double ordinate of hyperbola \[\dfrac{{{x^2}}}{{{a^2}}} - \dfrac{{{y^2}}}{{{b^2}}} = 1\] such that OPQ is an equilateral triangle, O being the center of hyperbola, where the eccentricity of the hyperbola \[e\] satisfy,\[\sqrt 3 e > k\], then the value of k is

Answer 1

Hint: Here we have to find the value of eccentricity of the hyperbola. We will first write the polar coordinates of the point P and point Q. Here it is given that the OPQ is an equilateral triangle. O is the center of the hyperbola; all the angles of the triangle will be \[60^\circ \]. Then we will apply the distance formula and eccentricity formula for hyperbola to get the value of k.

Complete step-by-step answer:
We will draw the figure first with appropriate data given.

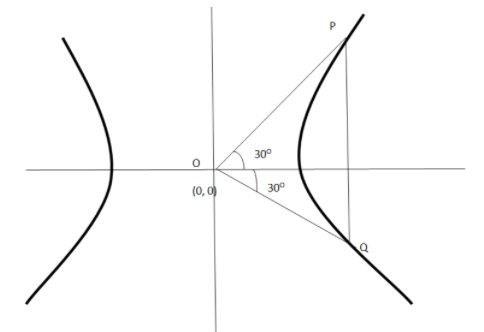
It is given that O is the center of the hyperbola and PQ is the double ordinate of the hyperbola. So the coordinate of point P \[ = \left( {a\sec \theta ,b\tan \theta } \right)\] and coordinate of Q \[ = \left( {a\sec \theta , - b\tan \theta } \right)\]
Since \[\Delta POQ\] is an equilateral triangle. So the length of all sides is equal. Thus, \[PO = QO = PQ\].
We will find the distance between these two points, \[\left( {a\sec \theta , - b\tan \theta } \right)\] and \[\left( {a\sec \theta ,b\tan \theta } \right)\].
Now we will replace \[{x_1}\] with \[a\sec \theta \], \[{y_1}\] with \[ - b\tan \theta \], \[{x_2}\] with \[a\sec \theta \] and \[{y_2}\] with \[b\tan \theta \] in the distance formula \[\sqrt {\left[ {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \right]} \].
Distance of the point \[\left( {a\sec \theta , - b\tan \theta } \right)\] from \[\left( {a\sec \theta ,b\tan \theta } \right)\]\[ = \sqrt {\left[ {{{\left( {a\sec \theta - a\sec \theta } \right)}^2} + {{\left( {b\tan \theta - ( - b\tan \theta )} \right)}^2}} \right]} \]
Subtracting the terms and applying exponents on the bases, we get
Distance of the point \[\left( {a\sec \theta , - b\tan \theta } \right)\]from \[\left( {a\sec \theta ,b\tan \theta } \right)\] \[ = \sqrt {0 + 4{b^2}{{\tan }^2}\theta } \] …………..\[\left( 1 \right)\]
Similarly, we will find the distance between the points \[\left( {0,0} \right)\] and \[\left( {a\sec \theta ,b\tan \theta } \right)\].
Now we will replace \[{x_1}\] with 0, \[{y_1}\] with 0, \[{x_2}\] with \[a\sec \theta \] and \[{y_2}\] with \[b\tan \theta \] in the distance formula \[\sqrt {\left[ {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}} \right]} \].
Distance of the point \[\left( {0,0} \right)\] from \[\left( {a\sec \theta ,b\tan \theta } \right)\] \[ = \sqrt {\left[ {{{\left( {a\sec \theta - 0} \right)}^2} + {{\left( {b\tan \theta - 0} \right)}^2}} \right]} \]
Applying exponents on the bases, we get
Distance of point \[\left( {0,0} \right)\] from \[\left( {a\sec \theta ,b\tan \theta } \right)\] \[ = \sqrt {{a^2}{{\sec }^2}\theta + {b^2}{{\tan }^2}\theta } \]………….\[\left( 2 \right)\]
Squaring and equating equation \[\left( 1 \right)\] and equation \[\left( 2 \right)\], we get
\[{\left( {\sqrt {0 + 4{b^2}{{\tan }^2}\theta } } \right)^2} = {\left( {\sqrt {{a^2}{{\sec }^2}\theta + {b^2}{{\tan }^2}\theta } } \right)^2}\]
Simplifying the equation, we get
$\Rightarrow$ \[4{a^2}{\tan ^2}\theta = {a^2}{\sec ^2}\theta + {a^2}{\tan ^2}\theta \]
Adding and subtracting like terms, we get
$\Rightarrow$ \[3{b^2}{\tan ^2}\theta = {a^2}{\sec ^2}\theta \]
On further simplification, we get
$\Rightarrow$ \[\dfrac{{{b^2}}}{{{a^2}}} = \dfrac{{{{\sec }^2}\theta }}{{3{{\tan }^2}\theta }}\]
Breaking the terms, we get
$\Rightarrow$ \[\dfrac{{{b^2}}}{{{a^2}}} = \dfrac{{\dfrac{1}{{{{\cos }^2}\theta }}}}{{\dfrac{{3{{\sin }^2}\theta }}{{{{\cos }^2}\theta }}}} = \dfrac{1}{{3{{\sin }^2}\theta }}\]
We know the square of eccentricity of hyperbola is equal to \[1 + \dfrac{{{b^2}}}{{{a^2}}}\] i.e. \[{e^2} = 1 + \dfrac{{{b^2}}}{{{a^2}}}\]
We will put the value of \[\dfrac{{{b^2}}}{{{a^2}}}\] that we have calculated, in the above formula.
$\Rightarrow$ \[{e^2} = 1 + \dfrac{1}{{3{{\sin }^2}\theta }}\]
Simplifying the terms further, we get
$\Rightarrow$ \[{e^2} = \dfrac{{1 + 4{{\tan }^2}\theta }}{{3{{\tan }^2}\theta }}\]
Rewriting the equation, we get
$\Rightarrow$ \[\dfrac{1}{{3\left( {{e^2} - 1} \right)}} = {\sin ^2}\theta \]
We know that \[{\sin ^2}\theta < 1\].
Therefore,
$\Rightarrow$ \[\dfrac{1}{{3\left( {{e^2} - 1} \right)}} < 1\]
Using inequality property, we get
$\Rightarrow$ \[3\left( {{e^2} - 1} \right) > 1\]
Simplifying the terms, we get
$\Rightarrow$ \[{e^2} - 1 > \dfrac{1}{3}\]
Adding 1 on both sides, we get
\[\Rightarrow {e^2} - 1 + 1 > \dfrac{1}{3} + 1\\ \Rightarrow {e^2} > \dfrac{4}{3}\]
Taking square root on both sides, we get
\[\Rightarrow \sqrt {{e^2}} > \sqrt {\dfrac{4}{3}} \\\Rightarrow e > \dfrac{2}{{\sqrt 3 }}\\\Rightarrow \sqrt 3 e > 2\]
Thus, the value of \[k\] is 2.

Note: We have found out the required answer using the eccentricity of hyperbola. Eccentricity is a measure that tells how much a conic section differs from being circular. Conic section includes the circle, hyperbola, parabola etc. Different conic sections have different eccentricity. For example, a circle has an eccentricity 0 whereas hyperbola has an eccentricity usually greater than 1. It therefore becomes very important to keep in mind the formula of eccentricity for different conic sections.